
Everyone thinks about it.
The CooperToons website deems it essential to answer the fundamental question of existence!
Just what the Hey is
Modal Logic?

Everyone thinks about it.
At one time or another, everyone puts down the remote, leans back in the recliner, takes another swig, and wonders:
"Just what the heck is modal logic?"
Then at half-time, you go to your Internet and look it up. Then you'll find definitions like:
 |
A logic with modality. |
Of course, you then go and look up what "modality" means. And you find:
 |
The quality or state of being modal. |
So naturally you now look up "modal":
 |
Of or relating to modality. |
And at this point you say, "Ha? (quoting Shakespeare). From this philosophers make a living?"
Indeed, they do. And if you want to learn more about this - ah - "mode" of employment, read on!
The Modal the Merrier
The word "mode" or "modal" is, we must admit, a bit vague. The Merriam-Webster Dictionary defines "mode" as "a particular form or variety of something." In other words, a mode is a kind of something.
So "modal" logics (and there are more than one type) must refer to a some kinds of logic. And specifically we learn that modal logics refer to some kinds of formal or symbolic logics.
Of course, everyone knows about symbolic logic. That's where you represent the words "not", "and", "or", and "if-then" with funny looking symbols like ¬, ∧, ∨, and →. You use these logical connectives to link atomic sentences to form larger sentences which are called molecular sentences.
Of course, it might help to explain what the terms mean. Atomic sentences are sentences that are not divided into smaller sentences. Most of the time they are small short sentences that don't contain the words "not", "and", "or", and "if-then". But not always. What matters is that when you use the sentences you don't split them up during the course of the argument.
For instance, we can use the simple letter G to represent the following:
| G | : | George Washington led the American Revolution. |
G, then, is the formal or symbolic representation of the atomic sentence, "George Washington led the American Revolution." In this case G happens to be TRUE.
Now suppose I define a new atomic sentence.
| R | : | Robespierre never came to power. |
This is another atomic sentence which happens to be FALSE.
OK. Now let's write a sentence combining both atomic sentences.
If George Washington led the American Revolution, then Robespierre never came to power.
This we can represent as:
G → R
... where the arrow, →, means IF-THEN.
The IF-THEN sentence, G → R, then, is the molecular sentence formed from the two atomic sentences, G and R.
We can now tidy up the grammar a bit, and we have the molecular IF-THEN sentence in plain English:
If George Washington had led the American Revolution, then Robespierre could never have come to power.
... a molecular sentence which is clearly FALSE.
So we see that with the IF-part (the antecedent) being TRUE and the THEN-part (the consequent) being FALSE, the whole IF-THEN sentence is FALSE.
TRUE → FALSE = FALSE
So ends our review of classical propositional logic.

Ain't Necessarily
It Ain't Necessarily So
The characteristic of classical propositional logic is that statements are TRUE or FALSE. And the truth or falsity of a molecular sentence depends only on the truth or falsity of the atomic sentences.
With only two truth values, if something is proven not to be TRUE, then it is FALSE. And if it is proven not to be FALSE, it defaults to being TRUE.
Unfortunately, natural language isn't so clear cut. In particular they way IF-THEN statements are used in symbolic logic doesn't always gibe with their use in natural language. And this is what led to the development of modal logic.
For instance, consider a statement like:
If George Washington had led the French Revolution then Robespierre would never have come to power.
Now most people would think this sentence might be FALSE. After all, both of the atomic sentences:
| G: | George Washington led the French Revolution. | ||||
| R: | Robespierre never came to power. |
... are FALSE. So we would think the whole IF-THEN sentence:
| G → R: | If George Washington led the French Revolution, then Robespierre never came to power. |
... would also be FALSE.
But according to logic the sentence is TRUE.
Ha? (Again Shakespeare.) How is that possible?
We have to be honest and say that IF-THEN statements have been fodder for philosophical discussion for - literally - thousands of years. If you want to see why such IF-THEN statements sometimes act in such an oddball fashion, you can read a separate essay on the topic if you just click here.
But we can also look at it in a simplistic manner. Remember in classical logic, sentences are only TRUE or FALSE. And we can't prove it is FALSE that if George led the French Revolution, then Robespierre would never have come to power. Since the sentence isn't FALSE, in classical logic by default it must be TRUE.
In fact, as long as the IF-part and the THEN-part are both FALSE, then an IF-THEN statement is TRUE. Although this is a bit hard to believe, a real-world example will show us there are conversational sentences where the FALSE → FALSE = TRUE criterion applies.
Consider this commonly used sentence:
If you think you're going to the rock concert on a weeknight, then I'll fly to the moon.
Clearly, the parents are asserting that what they say - the whole IF-THEN statement - is TRUE. But since they are also insuring the THEN-part is FALSE, they are telling the kids that the IF-part is likewise FALSE. So we have natural language examples of an IF-THEN statement which is TRUE, but where both the antecedent and consequent are FALSE.
But now consider this strange sentence:
If George Washington had discovered the Theory of Relativity then Robespierre would have been a 1960's pop artist.
... which is a FALSE → FALSE sentence.
And so it is TRUE!
So you can have TRUE IF-THEN statements where the IF-part and THEN-part, are both FALSE, but are absolute nonsense!
So what to do?
It IS Necessarily - and POSSIBLY So
OK. Let's again consider our sentence:
If George Washington led the French Revolution then Robespierre never came to power.
As we said, this is TRUE according to logic.
But consider this sentence:
IT IS NECESSARY THAT if George Washington led the French Revolution then Robespierre never came to power.
... TRUE or FALSE?
Well, clearly the statement is FALSE. So it seems that if we make IF-THEN statements in normal conversation, we are really asserting the IF-THEN statement is necessary if we mean it is TRUE.
This idea hit the famous logician, Clarence Irving Lewis, in 1912. So he proposed a new type of IF-THEN statement called strict implication to distinguish it from the material implication as the IF-THEN statements were called is classical logic.
And Clarence introduced the notion of necessity and used the symbol □. So his definition of strict implication is:
| It is necessary that if George Washington led the French Revolution then Robespierre never came to power. | = | □(G → R) |
By introducing the concept of necessity in his definition of strict implication, Clarence is considered the inventor of modern modal logic.
Although Clarence helped clarify the IF-THEN usage in normal language some, it didn't satisfy a lot of philosophers. Instead, they say that you still can't always tell if the sentence is TRUE or FALSE. The concept of necessity was strict and most things are not necessary - even if they really happen!
So if you think about it, maybe we should say:
It is possible if George Washington led the French Revolution then Robespierre never came to power.
For most people this statement seems to be TRUE.
On the other hand, it might be false. After all, George did stay in America. So in reality it is impossible for him to have led the French Revolution no matter who came to power.
So should the sentence really be FALSE? How do we decide?
The way out was provided by Professor Saul Kripke who is usually given credit for bringing modal logic into its current form. What Saul did was to ask if there is a possible world where George Washington did indeed lead the French Revolution. If there is such a possible world, then we say it is possible that George could have done it.
That naturally brings up the question. How do you determine if there is such a possible world?
Well, one way is simply to realize a world is possible if it is conceivable. So if you can picture a world where George led the French Revolution and Robespierre never came to power, then the IF-THEN sentence is indeed possible.
So with the notion of possibility we need a new symbol. And modal logic represents the concept of possibility with a diamond or lozenge, ◊.
| It is possible that if George Washington led the French Revolution then Robespierre never came to power. | = | ◊(G → R) |
The next step is to determine the exact relationship between the two symbols, ◊ and □.
It Ain't Necessarily Not Possibly So
Let's consider the nice simple statement.
George Washington did not lead the French Revolution.
And everyone who has taken symbolic logic knows, we write this as:
¬G
... where ¬ means "not" or "It is false that".
And now we slip in the possibility symbol, ◊:
¬◊G
What exactly does this mean?
Well, using the definition of our modal operator it means:
It is false that it is possible George Washington led the French Revolution.
... or more grammatically:
It is impossible for George Washington to have led the French Revolution.
And so we can now write:
¬◊
to mean "It is impossible".
Now look at this:
¬◊¬G
Clearly this means:
It is IMPOSSIBLE that George Washington DID NOT lead the French Revolution.
But exactly what does it mean that it is impossible that someone did not do something?
Well, it means they must have done it.
So...
¬◊¬G
...which is just another way of saying.
George Washington MUST have led the French Revolution.
And if someone must have done something, then it was NECESSARY for them to have done it.
So now we can define our sentence:
¬◊¬G
... to mean:
It is NECESSARY that George Washington led the French Revolution.
Ha! So the necessity symbol □ can be defined in terms of the possibility operator by:
□ = ¬◊¬
But then we again have to ask. Is the sentence ...
It is NECESSARY that George Washington led the French Revolution.
... TRUE or FALSE?
Well, let's go back to our possible worlds scenario. We can certainly picture a possible world where George did not lead the French revolution. In fact, he did not do so in our, the real world. But there's also a lot of other possible worlds where he didn't lead the French Revolution - such as the possible world where he went to England, signed up on the ship HMS Bounty, and retired to Tahiti.
So there are possible worlds where the sentence:
George Washington led the French Revolution.
is FALSE. Therefore it is not necessary that George led the French Revolution.
So the sentence is indeed FALSE.
But what about this sentence:
It is NECESSARY that George Washington led the American Revolution.
Well, you might think since it is TRUE in the real world, then it is necessary. That, though, is not the case.
Remember, we are using the possible worlds criteria for our modal logic - or rather the possible world semantics as we call Saul's approach. So can we picture a possible world where George did not lead the American Revolution - even though he did in the real world?
Of course. We just pictured such a world. In fact we have already done so: the possible world where George led the French Revolution.
So in modal logic we define necessity as something that must be true in all possible worlds. If there is even one possible world where the statement is not true, the sentence is FALSE. So we have to say that the sentence.
It is necessary that George Washington led the American Revolution.
... is FALSE.
What is important when moving ahead in modal logic is to realize that just because something is TRUE in our - the real world - does not mean it is necessarily TRUE.
So what, we now ask, is necessity in modal logic? Or rather is there anything that is necessarily necessary in all possible worlds?
Well, we do have sentences like:
It is necessary that 2 + 2 = 4
This sentence is TRUE in modal logic because 2 + 2 = 4 is TRUE in all possible worlds.
And a sentence like:
It is possible that 2 + 2 = 5
... is FALSE because that 2 + 2 = 5 is FALSE in all possible worlds.
In fact if anything can be proven to be TRUE using classical symbolic logic - which includes mathematics - then it is TRUE in all possible worlds. So if you can prove a statement - call it p - to be TRUE in traditional symbolic logic, then □p is TRUE is modal logic as well.
It Ain't Not Possibly Not Necessarily So
And at this point the readers again may scratch their heads as say, "From this, philosophers make a living?
But wait a minute, the modal logicians say. You need philosophers to explain subtle nuances of logic - modal or otherwise. For instance, suppose we want to say it was not necessary for George to have led the French Revolution. We would write:
¬□G
Now in everyday English, we would say if something was not necessary, it still might be possible. So we would think we should be able to write:
¬□G = ◊G
But oddly enough, this isn't correct. To prove this we need to review a point of classical propositional logic.
In classical logic, there is what they call the contrapositive of an "If-Then" Statement.
Consider this sentence:
If he is George Washington, then he is the Father of His Country.
Note, though, that this means the same thing as:
If he is NOT the Father of His Country, then he is NOT George Washington.
Or at least, both sentences are TRUE or FALSE at the same time. That is, they have identical TRUTH VALUES and so we represent the contrapositives by writing:
G → F ⇔ ¬F → ¬G
Since we can apply the contrapositive to modal logic, we have the following equivalence as well:
| ¬□G → ◊G | ⇔ | ¬◊G → ¬¬□G |
.. and start manipulating the symbols by accepted rules.
| ¬□G | → | ◊G | IF-THEN Statement | ||||||||
| ¬◊G | → | ¬¬□G | Contrapositive | ||||||||
| ¬◊G | → | □G | Double "nots" (¬¬) Cancel |
The final sentence is then:
¬◊G → □G
But this means:
If something is not possible, then it is necessary.
But this obviously is not correct. So we cannot say that if something is not necessary then it is still possible. At least not in modal logic.
The point here is that in modal logic, the terms possibility and necessity are not exactly what we mean in everyday English. The necessity operator, □ is the strong operator and encompasses the weak operator, possibility, ◊
The easy way out is to simply define possibility as:
◊ = ¬□¬
... and just accept the words don't mean exactly the same thing as in everyday English.
So we have what are called reciprocal definitions of the modal operators, ◊ and □, as:
◊ = ¬□¬
□ = ¬◊¬
Which if nothing else are easy to remember.
The Postulates
"You can prove anything you want by coldly logical reason - if you pick the proper postulates." - Isaac Asimov (I, Robot).
Great. After all this work, we've arrived at the conclusion we need to correct old-fashioned non-modal logic because it doesn't match everyday language. So we invent a modal logic which doesn't match everyday language either.
So what do we do?
Whenever mathematicians and logicians get backed into a corner because you can no longer draw parallels with the real world, they have a slick trick. They axiomize their system. That is they create a series of basic statements called axioms or postulates. Axioms are (usually) simple statements that are fundamental to the system and are accepted as TRUE. If people don't believe the axioms or the axioms don't make sense, well, that's just tough tiddy.
Modal logic is no different and the first modal axiom is actually pretty simple - if you know classical logic. In fact it's so simple we call it Axiom 0.
| Axiom 0: | All postulates, symbols, and rules of classical logic are postulates, symbols, and rules of modal logic. |
So the second axiom - which we call Axiom 1 - is the first axiom of modal logic that we don't have in classical logic.
| Axiom 1: | □p → p | If p is NECESSARILY TRUE, then p is TRUE. |
This axiom is fundamental to modal logic. That is, if something is TRUE in all possible worlds, then it is TRUE - no ifs, ands, or buts.
Now you would think the opposite is TRUE as well.
| p → □p | (An Axiom?) | ||
But this is not in general an axiom of modal logic, although as we'll see below, it can be a premise in particular proofs.
Axiom #2 is not as obvious as Axiom #1.
| Axiom 2: | □(p → q) → (□p → □q) | If it is necessary that p implies q, then if p is necessary then q is necessary. |
That is, the operator, □, distributes over the IF-THEN statement.
This axiom is borrowed from natural language. If we say "It is necessary that if George Washington led the French Revolution then Robespierre would never have come to power" we can also say "If it is necessary that George Washington led the French Revolution then it is necessary that Robespierre would never have come to power."
A word of warning. Although
□(p → q) → (□p → □q)
... is TRUE, the opposite:
(□p → □q) → □(p → q)
... is NOT TRUE. There is, though, a related equation we'll show below that is correct.
It's Axiom #3 that begins to raise eyebrows.
| Axiom 3: | □p → □□p | If p is NECESSARY, then it is NECESSARY that p is NECESSARY. |
And to make things even more verbose, we have Axiom #4.
| Axiom 4: | ◊p → □◊p | If p is POSSIBLE, then it is NECESSARY that p is POSSIBLE. |
Axioms 3 and 4 are sometimes lumped together as Becker's Postulate, named after mathematician and logician Oskar Becker. Both postulates state that a modal operator is always necessary.
Now if you want another axiom we can supply it:
| Axiom 5: | p → □◊p | If p is TRUE, then it is NECESSARY that p is POSSIBLE. |
Finally we return to what we said at first about necessity. If a formula is derivable from non-modal logic - that is, good old-fashioned symbolic logic - then the formula is necessary in modal logic. This is called the necessitation rule and is written as:
⊢p, ⊢□p
The symbol, ⊢, - sometimes called a "turnstile" by philosophers - means that the symbol that follows represents either an axiom or a formula that can be derived as a theorem. So we're saying if a sentence is derivable in regular logic, then we have a theorem in modal logic that the sentence is necessarily true.
Note that our necessitation rule does not mean:
p → □p
... if p is a formula derivable in modal logic. The necessiation rule applies only if p is derivable in non-modal classical symbolic logic. This point is so subtle that the necessitation rule is often not listed with the modal logic axioms but is simply understood to be true.
Now for some reasons, modal philosophers don't like working just with numbers. Instead, they use letters and numbers to name the axioms. So in some places you'll find lists of axioms like:
| Necessitation Rule | ⊢p, ⊢□p | |||
| K: | □(p → q) → (□p → □q) | |||
| M: | □p → p | |||
| 4: | □p → □□p | |||
| 5: | ◊□p → □◊p | |||
| B: | p → □◊p |
These axioms are lumped together in various ways to form systems of modal logic. In brief these systems are:
| System | Axioms |
| K | Necessitation Rule and Axiom K |
| M | System K and Axiom M |
| S4 | System M and Axiom 4 |
| S5 | System S4 and Axiom 5 |
| B | System M and Axiom B |
For those interested in the history of logic, System K is named in honor of Saul Kripke and System B in honor of the mathematician and logician Luitzen Brouwer.
And now, as the $100 an hour psychiatrist said, we can begin, yes?
A Matter of Opinion

Bertie didn't buy it.
There is no one fundamental logical notion of necessity, nor consequently of possibility. The subject of modality ought to be banished from logic. "
- Bertrand Russell
Abbreviated from "Necessity and Possibility", 1905, 65th Meeting of the Society of Old Bursary, Exeter College, Cambridge University, 1905.
Well, we can't say that Bertie was correct - not necessarily. (If you're not a philosopher, that was a joke, by the way.)
But a word of warning is in order. You might think that modal logic axioms are accepted by everyone just like (most) everyone accepts Euclid's axioms. But that's not the case. Not only will you find differences of opinion on what are acceptable axioms but even what are valid theorems. And we're not just talking about the fact there are different types of modal logics.
For instance, you might wonder about proving:
□p → ◊p
After all if something is TRUE in all possible worlds it must be TRUE in at least one possible world.
And yes, you may find a discussion about modal logic where some student asked the question on how to prove this statement.
But instead of the proof you might get at best a rather archly stated comment and at worse a spittle-flinging diatribe that the statement can't be proven because the formula in invalid.
And yet in the discussion we find that someone else proves the statmement is valid - but in a way no one can understand.
But then someone else in the discussion says you can't prove the statement because it's an axiom!
What, as Flakey Foont asked Mr. Natural, does it all mean?

Profound Truths
For the Good of Mankind
So, we ask, just what good is modal logic?
Well, let's again list all the axioms that are often accepted.
| Necessitation Rule | ⊢p, ⊢□p | |||
| K: | □(p → q) → (□p → □q) | |||
| M: | □p → p | |||
| 4: | □p → □□p | |||
| 5: | ◊□p → □◊p | |||
| B: | p → □◊p |
It turns out logicians have applied these axioms to a lot of things, and not just to figure if something is necessary or possible. One modal logic application is epistemology. That is, how do we distinguish if someone simply believes something or knows something.
For instance we let, ◊p mean "Someone believes p". Then we let □p mean "Someone knows p." And p itself simply means "p is TRUE".
You can see how the axioms work. So when we say:
□p → p
... we are using Axiom M. But in epistemic modal logic this means:
If someone knows p, then p is TRUE.
... which some people may question. But this point is fundamental to distinguishing belief from knowledge.
For instance in epistemic logic we also know:
◊p → ¬□p
That is, just believing you know something doesn't make it TRUE.
But at least, you say, with epistemic modal logic, now we must be able to distinguish belief from knoweldge, and so determine if a statement is true in an absolute sense.
Correct?
Uh, sorry. We can't say that.
In fact, you'll find philosophers are still arguing.
There's one weird thing about the various logics. They never quite do exactly what the philosophers want them to do. But then they are quickly appropriated by engineers and scientists from other fields where they work quite nicely, thank you.
For instance it was in the mid-19th century that George Boole began developing symbolic logic to clarify the way people think. Of course George's Boolean Algebra helped philosophers a little - it led to modern symbolic logic. But we also know that philosophers have kept working with George's system and yet they keep arguing about the things they've been arguing about for thousands of years. So they keep inventing more logics!
On the other hand, George's Algebra in its earliest form had a major impact on the fields of electrical engineering and computer circuit design. For instance, if you have a circuit like:
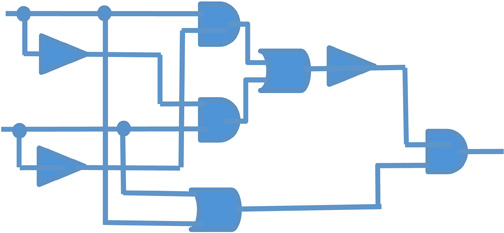
Circuit #1
... Boolean Algebra shows that this is equivalent to:

Circuit #2
... which is quite a simplification.
So with Boolean Algebra we can combine a number of complex circuits and then simplify them to make them smaller. Then with the advances in physical miniaturization of electronics, we now have computers sitting in the privacy of our own homes that can outperform the supercomputers of thirty years ago.
In a similar way modal logic has been quite a help to computer scientists as well. This is because once the Curry-Howard Equivalence of programming and logic was discovered (no, we aren't mispronouncing the name of one of the Stooges) what seemed to be esoteric systems of logic were found to represent generalized methods of programming computers.
It turns out that terms and relations of modal logic have exact and definite equivalences to terms and relations in computer science. For instance, if you link a bunch of computers together, they can be considered as hypothetical worlds and so modal logic can model specific interactions and relationships of the various servers with each other. One important field of such applications has been in the field of computer security.
Well, that's fine. But if you're a philosopher what can you do with modal logic? Other than prove that if something is not necessary then you can't say it's possible?
Well, let's look at a famous modal argument. Like many arguments, we start of with premises - that is assumptions that are not necessarily in our axioms:
| p → □p | Premise 1 | If p is TRUE, then p is necessary. | |||||
| ◊p | Premise 2 | p is possible. |
Now we're not saying what p is just yet. And there's one more modal rule that is helpful.
If you remember about contrapositives, you'll remember these two terms are equivalent,
p → q = ¬q → ¬p
But since both equations are from symbolic logic - not just modal logic - we can apply the necessitation rule and add necessity to both sides of the equation:
Now with the necessistation rules we know if something is derivable in non-modal logic then it is also necessary.
⊢p, ⊢□p
So we can substitute p with any other formula. So we substitute the formula (p → q):
(p → q) → □(p → q)
And take the contrapositive of (p → q):
(¬q → ¬p)
And substitute it on the right side:
(p → q) → (¬q → ¬p)
Since the contrapositive ¬q → ¬p is derived using classical logic, by the necessitation rule we also have:
⊢(¬q → ¬p), ⊢□(¬q → ¬p)
So we can now write:
(p → q) → □(¬q → ¬p)
Then using Axiom K:
(p → q) → (□¬q → □¬p)
This is called Modal Modus Tollens.
Remember we said that p → q had to be derivable from classical logic. However, you can use Modal Modus Tollens on modal formulas if 1) it is a PREMISE of the argument, an AXIOM of the system, or 3) you properly derive the formula from the premises or the axioms. So we can use it in our proof.
So off we go:
| 1 | p → □p | Premise 1 | If p, necessarily p. | |||
| 2 | ◊p | Premise 2 | p is possible. | |||
| 3 | ¬□p → □¬□p | Substitution of ¬□p for p in Premise 1 (Step 1). (Valid formulas can be substituted for each other.) | If p is not necessary then it is necessary that p is not necessary. | |||
| 4 | (p → □p) → (□¬□p → □¬p) | Modal Version of Modus Tollens on Premise 1 (Step 1): (p → q) → (□¬q → □¬p) | If p implies necessarily p then necessarily not necessarily p then necessarily not p. | |||
| 5 | □¬□p → □¬p | "Classical" Modus Ponens on Step 4 using Premise 1 (Step 1): (p → q) and q, then p | If necessarily not necessarily p then necessarily not p. | |||
| 6 | ¬□p → □¬p | Hypothetical Syllogism of Steps 3 and 5: If p → q and q → r, then it follows p → r | If not necessarily p then it is necessary that not p. | |||
| 7 | ¬¬□p ∨ □¬p | Equivalent of "Not-Or" with "If-Then" in Step 6. | p is necessary or it is necessary that not p. | |||
| 8 | □p ∨ □¬p | Double "Nots" cancel in Step 7. | p is necessary or it is necessary that not p. | |||
| 9 | ¬□¬p | Premise 2 (Step 2) and Equivalence of ◊ = ¬□¬ | Not necessarily not p. | |||
| 10 | □p | Disjunctive Syllogism of Steps 9 and 10: If p ∨ q and ¬q, then p | p is necessary. | |||
| 11 | p | Modus Ponens on Step 10 with Step 1 (Premise 1): If p → q and q, then p | p is TRUE. |
OK, we start out with premises that have a statement p. We do a lot of hocus-pocus and end up proving p
.So what good is this stuff?
Well, in this case that depends on what we mean by p.
There's one interpretation of this proof that's pretty famous. That's when you define p as "There exists an ultimate perfect being". And hey, presto!, you've just proven that ultimate perfect being" exists. So this is an example of the Modal Ontological Argument and this form - or its equivalent - was first devised by the long-lived philosopher and theologian, Charles Hartshorne.
But yes, there are not a lot of people who think this is a convincing proof ultimate perfect being exits. The problem of whether an argumentis is TRUE, boils down to to two quesitons:
Is the logic correct?
Here the answer is yes.
And are the premises TRUE?
That's where we run into trouble.
After all, remember our Premise 1:
p → □p
This is essentially the necessitation rule, but expressed as a formula of modal logic. This premise, then, let's us assume something that is normally TRUE for theorems of classical propositional logic can also be used for all modal sentences. To some this looks like we've snuck in a disguised circular argument.
Also, the second premise says that p is possible. True, if you define p as something simple like "George Washington was King of France", you can see it as being possible. But if you define p as ultimate perfection, this is more questionable and again comes off as disguise circularity.
In general, the premises state that "[Something] exists as long as you accept IF it exists then it NECESSARILY exists, and it is POSSIBLE it exists". When stated like this, they come off as very wishy-washy. You can, in fact, stick in almost anything for p.
If you believe that "Absolute Knowledge exits then it necessarily exists, and "Absolute Knowledge is possible" then you can prove Absolute Knowledge exists. But try this with something like "The Ultimate Chocloate Cake", or "The Biggest Jerk for a Boss". These also work.
SO MODAL LOGIC!!!!! WHAT GOOD IS IT????!!!!????
All right, all right. Some fields other than philosophy that have found practical uses of modal logic today. Examples are:
One specific example where using modal logic has become useful is in mathematical proof theory. That is, proving things about mathematical proofs. A good starting place for the provability logic is:
| Necessitation Rule | ⊢p, ⊢□p | |||
| K: | □(p → q) → (□p → □q) | |||
| M: | □p → p | |||
| L: | □(□p → p) → p |
The L Axiom is named for the German mathematician Martin Löb who thought it up. You need this for proofs about proofs although you don't find it in other modal logics.
Of course, in provability modal logic the two modal operators have a new meaning:
| □p | p is provable. | ||||
| ◊p | p is consistent. |
Now if p means "p is true", then □p means "It is provable that p is TRUE." But ◊p does not means "It is not provable that p is TRUE.
Remember that in all our modal logics:
◊p = ¬□¬p
... and so in proof theory modal logic ◊p means "It is false that p is not true is provable." Or more grammatically "It is unprovable that p is false." But exactly what does it mean if something is unprovable that it is false? Well, it means that p is consistent with the other statements of your system. And so we've labeled it as such.
You can get an idea how the modal axioms fit in with proof theory. For instance, we know that a basic modal axiom is Axiom M:
□p → p
Now in the normal modal logic this means "If p is necessary then p is TRUE". But in proof theory modal logic this means "If p is provable then p is TRUE." That makes sense. After all, you should be able only to prove things that are TRUE.
But on the other hand, consider this statement we've seen before.
p → □p
In our early modal logic, this meant if p is TRUE then p is necessary. But remember we said this is not normally a proper axiom in model logic. Still, when talking about necessity, this still seems like it should be TRUE.
And if we're talking about the proof theory, in modal logic this should mean, "If p is TRUE then p is provable." And again this is something that you might think should be TRUE. So one more we thing p → □p should be an axiom.

Kurt Gödel
He's famous.
But it turns out this isn't the case. You probably know about Kurt Gödel, the famous mathematician. Despite what you read, Kurt did not prove there were GREAT UNKNOWABLE TRUTHS that cannot be proven. What he did do was prove that if you load up a mathematical system with enough symbols and rules, you can write more formulas than you have theorems to prove them with.
If you've tried to read Kurt's paper, it's pretty tough going (you can read a sketchy outline if you click here). And that's where modal logic simplifies things.
Kurt showed everyone that you can indeed have true statements which are not provable. Simple arithmetic with addition, subtraction, multiplication, and division is such a system.
So we see that p → □p is indeed not something to assume as a general axiom. True, there are some systems where you can prove all TRUE statements. For instance, formal classical propositional logic - symbolic logic where the letters stand for atomic sentences - is such a system. So with propositional logic we can say "If p is TRUE then p is provable. But you can't in general assume p → □p is TRUE for all systems.
In any case, as time has gone on, more and more people have seen that modal logic is a help to philosophy, mathematics, and related fields. And yes, quite a few people make a living at it.
References
Sadly, there does not seem to be anything like an Ignoramuses Guide to Modal Logic and most textbooks, even elementary ones, might be tough going for the armchair philosopher. Also some of the books - too typical of textbooks today - are absurdly overpriced, no doubt due to the bean counters of the book publishers sitting down with their spreadsheets trying to figure how to get the bosses their projected bonuses.
The CooperToons policy is not to cite reference books with exorbitant prices (even some e-books sell for hundreds of dollars). Fortunately, in most towns there are these buildings called libraries where you can, believe it or not, just walk in and borrow the books for free.
If the library doesn't have the book, then you can get an interlibrary loan. Again these are usually free and the librarians - usually nice helpful friendly ladies - can almost always find what you want.
There are also some decent on-line introductions which may still be accessible. One of the best has been a website by Professor Klement of the University of Massachusetts for a modal logic philosophy course he taught a number of years ago. Getting through the information, though, requires a good knowledge of classical symbolic logic.
A Brief Introduction to Modal Logic, Joel McCance. PDF Web. A good introduction to get you used to the symbolism of modern papers.
Basic Concepts in Modal Logic, Edward Zalta, Center for the Study of Language and Information Stanford University, PDF Format. Another good introduction.
Modal Logic of Strict Necessity and Possibility, O-Texts. Web. An online text book.
Modal Logic, Kevin Klement, http://courses.umass.edu/phil511/. Hopefully Professor Klement won't mind the listing of this page. The course used the textbook Modal Logic for Philosophers by James Garson, a book that is - again personal opinion - a bit pricey for the recreational philosopher but not absurdly so. Used editions are not too costly.
"Modal Logic", Stanford Encyclopedia of Logic, May 27, 2014, Web. Stanford Encyclopedia is a good starting place. It is written by experts.
"Charles Hartshorne", Stanford Encyclopedia of Logic, February 7, 2013.
"Applications of Modal Logic in Linguistics", Lawrence Moss and Hans Joerg Tiede Handbook of Modal Logic, Volume 3, Editors: Patrick Blackburn, Johan van Benthem, and Frank Wolter, Elsevier (2007) .
The Merriam-Webster Dictionary, Merriam-Webster, Inc., 2016. Looking up "mode", "modality", or "modal" is kind of like the BC comic strip where BC was looking up a word in Wiley's Dictionary.
"The Ontological Argument", Peter Suber, Earlham College, Web. https://legacy.earlham.edu/~peters/courses/re/onto-arg.htm. This version is probably the simplest to udnerstand. Peter states clearly that the original argument is Charles Hartshorne's and he made some slight modifications. The CooperToons version is a modification of Peter version
Kurt Gödel's Ontological Argument, Christopher Small, University of Waterloo, http://www.stats.uwaterloo.ca/~cgsmall/ontology1.html. Another discussion of the modal Ontological argument.
"Necessity and Possibility", Bertrand Russell, The Collected Papers of Bertrand Russell: Volume 4: Foundations of Logic, 1903-05, Bertrand Russell, Editor: Alasdair Urquhart (with assistance of Albert Lewis), Routledge, 1994.
"Modal Logic and Its Applications", Kit Fine, Mathematical Concepts and Foundations, Volume 3
I, Robot, Isaac Asimov, Doubleday, 1950.
Presentations, Papers, and Discussions from XXXXXXXX at YYYYYYYY on ZZZZZZZZ. It's probably best to be generic on some of the references.