The Monty Hall Problem Explained Clearly!
(With a spreadsheet solution thrown in as a bonus)

Not quite the Monty Hall Problem
A Most Controversial Question
If you want to get a rise out of your egghead friends, pose to them the Monty Hall Problem. Unless they've heard it before, they're bound to get it wrong. Then gratifyingly they will show themselves to be complete שמענדריקים by refusing to believe the correct answer even when shown the simple reasoning.
The Monty Hall Problem is based on the television show Let's Make a Deal. This show debuted in 1963 and starred - of course, Monty Hall - who at the time of this writing is venerable, but hale and well. When Monty took up the microphone on the pilot show, he probably had no idea that his name would be forever linked with a classic and controversial math problem. (For what it's worth, the show Let's Make a Deal - also at this writing - is still going strong.)
In the problem you have three doors. One door conceals a Grand Prize (like a car) and the other doors hide two identical Booby Prizes (like two donkeys).
The contestant then selects one of the doors. Next, Monty opens one of the other doors, revealing one of the donkeys. The contestant then must decide whether to stick with the first selection or to switch to the other unopened door.
What should the contestant do?
Most people say it doesn't' matter and reason this way. The contestants don't know where the Grand Prize is and so the odds are 1 out of 3 (1/3 or 33 %) they'll pick the right door. Then once the door is opened, the odds change to 50/50. So it doesn't matter.
The real answer, though, is the contestants should always switch. If they switch, the odds actually change. By sticking with their first choice, the odds remain at 1/3 (33 %) to win the Grand Prize. If they change doors, the odds go up to 2/3 or 66.7 %. But as we said, virtually no one believes this is the true answer.
The "Classic" Problem.
The Monty Hall Problem - as opposed to the Let's Make a Deal game show - was formulated in 1975. It was published in an article in American Statistician Magazine by mathematician Peter Sellvin. Peter gave the correct answer that you should always switch.
However, an equivalent problem - called the "Three Prisoners" - was published in 1957 in Martin Gardner's Mathematical Games column in Scientific American. The Three Prisoners, though, is a bit more complex in its presentation, and the connection between the Prisoners and the Monty Hall Problem isn't immediately obvious.
However, it wasn't until 1990 that the Monty Hall Problem hit its true international notoriety when it appeared in Parade magazine in the "Ask Marilyn" column by Marilyn Vos Savant. A reader sent in the question, and Marilyn responded with the correct answer (you should switch). She then added a brief explanation.
Evidently the explanation was too brief for quite a few mathematics professors to follow, and Marilyn was bombarded with many a spittle flinging diatribe how her published answer was complete נאַרישק. Unfortunately (for hundreds of Ph. D. mathematicians) Marilyn's answer was right.
The Simple Truth
It's really pretty simple to show that for the Classic Monty Hall Problem, switching is the best strategy. But to understand it with minimal effort, you really should - as is common in statistical or probability problems - work backwards. Don't think about determining the probability you will pick the Grand Prize. Focus on how likely it is to pick the Booby Prize(s). That makes things much simpler. But we'll still go though it step-by-step.
First clearly the likelihood of you picking the donkey - ergo, the Booby Prize - on the first try is indeed 2/3. You have two donkeys and one car. So the odds are 2/3 you'll pick the Booby Prize.
Next Monty must open a door with the other donkey. After all, he can't reveal the where the Grand Prize is.
But since 2/3 of the time, you have already picked one donkey, that also means 2/3 of the time - and pardon us if we shout - THE DOOR MONTY LEAVES SHUT MUST BE THE GRAND PRIZE!
Monty now asks, "Do you want to switch?" But this is equivalent to asking, "Do you want to stick with the door that has 2/3 probability of being a donkey, or select the other door that I didn't open and which has 2/3 chance of being the Grand Prize?"
To refuse to pick the other door - that is, to refuse to switch - is crazy, since 2/3 of the time it conceals the Grand Prize.
That's all there is to the Monty Hall Problem whose solution leads us to the 11th Commandment.
Thou shalt always switch.
Making It More Difficult
This last explanation is both correct and simple. But it rarely satisfies the Monty Hall Skeptics who will usually go off into tirades that make the most calm rational explanation of Stephen Fry seem like the expostulations of Donald Duck in one of his most extreme temper tantrums.
Perhaps because simple explanations lack credibility while complex and long winded pontifications are believed, the Monty Hall Problem is usually explained in terms of conditional probability. True, this requires understanding of the basic math of probability theory, but the actual arithmetic is pretty simple and doesn't go beyond what you had in middle school.
As we said, there are two donkeys and three doors, and the odds of picking a donkey - the Booby Prize - on the first selection is 2 out of 3 or 2/3. At this point Monty opens a door showing the other donkey.
Now if you picked one of the donkeys and you switched, the odds are a certainty (a probability of 1 or 100 %) that you will pick the door with the Grand Prize. So the overall probability of picking a Grand Prize in this case is
Overall Probability = (Probability of Step 1) × (Probability of Step 2 If Step 1 Occurs)
= 2/3 X 1 = 2/3 = 66.7 %
But what if you pick the door with the Grand Prize and you then switch? Well, the odds of picking the Grand Prize on the first pick is 1/3. Again Monty must open one of the doors, and of course it must be one of the donkeys. Therefore if you switch, then you would would pick the other donkey. So the overall probability of getting the Grand Prize is:
= 1/3 X 0 = 0
That is, a big fat zero.
This means regardless of whether you pick a donkey or the Grand Prize, if you switch the odds of getting the Grand Prize is:
2/3 + 0 = 2/3 or 66.7 %.
So eins mehr, we see you should always switch.
Although it's not necessary you can calculate what happens if you don't switch. Again it's 1/3 probability you pick the Grand Prize on your first pick. Don't switch and it's probability of 1 that you'll get the Grand Prize. So the overall probability you'll get the Grand Prize if you don't switch is:
= 1/3 X 1 = 1/3 = 33.3 %
Of course, if you pick the donkey first and don't switch, then you'll have a 0 % chance of getting the Grand Prize. So all in all, don't switch and you'll have
1/3 + 0 = 1/3 or 33.3 % chance
of landing the Grand Prize.
This agrees with the earlier conclusion. Always switch and you win 2/3 of the time.
It's popular to put conditional probability problems into tree diagrams. The odds for all cases mapped out and combined to get the overall odds. And you can't get a much simpler tree diagram than that of the Classic Monty Hall Problem.

The Monty Hall Problem for the Empirical
But when explained with this clear, concise, simple, and correct reasoning, many people still don't buy the answer. It seems you are mixing up different types of probabilities (which you are) and so the argument isn't valid (although it is). But mostly it's just too strange an answer to believe. So how can you prove the truth to Monty Hall Skeptics?
One surprisingly convincing demonstration (although not really a proof) is simply to play the game. Do this by taking two low ranking cards (like the Two of Clubs and the Two of Spades ) for the Booby Prizes - and a high ranking card like the Ace of Hearts for the Grand Prize and just play the game over and over. But just keep track of how many times you win and see who wins most of the time. The "contestants" will eventually come out ahead provided they always switches.
Unfortunately, you have to play the game quite a few times before the number of wins converges in a convincing manner to the final percentage of 2/3. If you play it ten times, due to the small sample size, the numbers will bounce all of the place. You might win only 4 times despite the expectation value being between 6 and 7 times. Unfortunately playing the game, say, 100 times can get a bit tedious and even then the total might be quite a bit off from the requisite 66.66666666666666666666667 % wins.
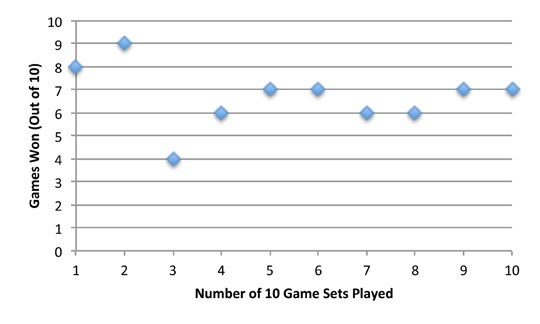

So if you want to take an empirical approach, the best way is to turn to the computer. Of course when the problem was posed in 1975, personal computers were not quite on the horizon (the Apple II went on the market two years later). But today we can easily demonstrate the soundness of the Monty Hall Answer (ergo, it is logically correct and true) with this now commonplace household appliance.
The computer method we use has the homonymously sounding name of the Monte Carlo method. In essence you have the computer play the Monty Hall Game many times and keep tabs of how often you win. So we'll have the computer play the game hundreds and even thousands of times. The computer will always switch doors, and then we'll see if it does indeed win 2/3 of the time.
Sadly, just telling someone that a computer - quote - "proves" - unquote - that we should switch isn't always convincing. After all, the programmer could have diddled with the program (or more charitably, he may have made a mistake). Today, though, there are more transparent and checkable ways to solve math problems.
In particular we have the ubiquitous spreadsheet. Spreadsheets are available from a number of companies, and some are even free. Also most of the sheets have the basic functions we will need, and better yet, spreadsheets let us run calculations hundred and even thousands of times. Best of all using a spreadsheet keeps the calculations in full view at all times.
So we'll set up the problem.
First we randomly pick a number from 1 to 3. Doing this represents the hiding the Grand Prize behind one of the doors. We'll put this number in the spreadsheet Cell #1.
There's several ways to do randomly pick the number. Some spreadsheets simply use a RANDBETWEEN function to generate a random number between two values. To randomly pick a number from 1 to 3 and put it in Cell #1 you just write into Cell #1.
=RANDBETWEEN(1,3)
If your spreadsheet doesn't have the RANDTWEEN function, it probably will have a function like RAN() or RAND() which generates a random real number between 0 and 1. You can generate a whole number from 1 to 3 in Cell #1 by the following equation:
=INT(RAND()*3) + 1
Because the INT function rounds a number down, you have to add then 1 at the end.
Next the contestant picks a door. To do this we just generate another random number from 1 to 3 using the same formula. This number we put into Cell 2.
For the third step we have to let Monty open a door. Here things get a bit trickier. The door Monty opens cannot be the door the contestant picked, nor can it be the door with the Grand Prize. Specifically, if the contestant picked the Grand Prize, Monty should randomly select one of the two other doors with a donkey. On the other hand, if the contestant picked a donkey, Monty has no discretion at all and must pick the door with the other donkey and leave the door with the Grand Prize closed.
Now for the Real Monty to open the correct door was pretty simple. The human brain can make decisions like this without problem. But for a computer to handle this step, we have to use a nested conditional equation in the spreadsheet. The equation must generate one of three numbers, but avoid the numbers assigned to the Grand Prize and the door the contestant selected.
But, of course since spreadsheets are now used in middle school math classes, it should be completely obvious to all but the most dense to see that all we need to do is take the following equation:
=IF(CELL2=CELL1,IF(CELL1=1,IF(RAND()<0.5, 2,3),IF(CELL1=3,IF(RAND()<0.5, 1,2),IF(RAND()<0.5,1,3))),IF(CELL2=1,IF(CELL1=2,3,2),IF(CELL2=2,IF(CELL1=1,3,1),IF(CELL1=2,1,2))))
and put it in Cell 3.
So this is the door that Monty opens.
Note that when Monty has the 50/50 opportunity to make one out of two selections - say Door 2 or 3 - you use the following equation:
IF(RAND()<0.5, 2,3)
to make the selection.
Of course, in writing the actual spreadsheet, what we are calling CELL1, CELL2, AND CELL3 have to be replaced with the actual cell references of the spreadsheet (which have names like A1, B2, AXZ123).
If it isn't obvious that using the above equation will simulate Monty opening the door, as an American president once said, "Trust me."
The contestant has now made a selection, Monty has opened a door, and the Grand Prize is hidden behind its door. At this point, your spreadsheet should look something like:

The Monty Hall Spreadsheet: Step 1
Now we are at the point where we ask if the contestant wants to switch or not. But since we are calculating what happens if the contestant does switch, then we will have the contestant always switch.
Of course, the door cannot be the one that Monty opened, and it can't be the one that the contestant first picked. Obviously - as all will clearly recognize - this requires the equation:.
=IF(CELL3=1,IF(CELL2=2,3,2),IF(CELL3=2,IF(CELL2=1,3,1),IF(CELL2=1,2,1)))
to be put into Cell 4.
So now the spreadsheet looks like:
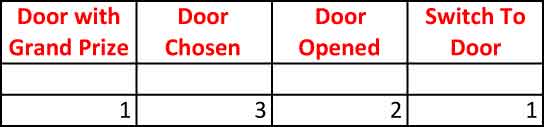
The Monty Hall Spreadsheet: Step 2
Now the final door selection has been made, so we'll check to see if it was the Grand Prize. Of course, we can just look at the spreadsheet and see that the door selected is the Grand Prize. That is, we see that CELL1 and CELL4 have the same number. But you also want to keep tabs of the number of times you correctly pick the Grand prize. So we put a number 1 into Cell 5 if the door numbers match. Otherwise we put in a 0. You do this by writing the equation:
=IF(CELL4=CELL5,1,0)
and put it into Cell 6. This lets us keep track of when the contestant has won or not. If he won, the cell has a 1, if not, the cell has a zero.

The Monty Hall Spreadsheet: Step 3
All of these cells are put into a single line, a line which represents one play in the Monty Hall Problem. We now copy and replicate this line down the spreadsheet - that is, we select the line with the mouse and drag the selection down - for, say, 1000 times. So we now have a spreadsheet with 1000 Monty Hall problems, each played independently of the other.
Finally we simply sum up the column with all the Cell 5's. This will be the total number of games where you won the Grand Prize. So in Cell 67 we write:
=SUM(CELL5_NUMBER1:CELL5_NUMBER_1000)
where, of course, where we must write =SUM(CELL5_NUMBER1:CELL5_NUMBER_1000) has to be replaced with the specific cells, say something like SUM(E3:E10002). Then we get the percentage of wins by dividing the number in Cell 6 by 10.
So in the end we have our Monty Hall Spreadsheet:
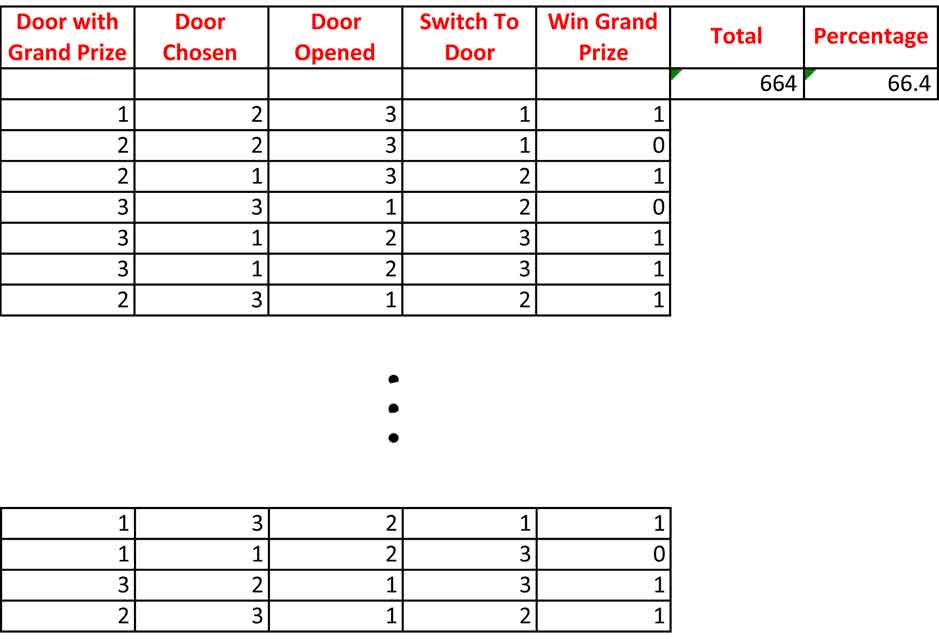
The Monty Hall Spreadsheet: Step 4
If you click here, you'll open up an example of the output, and you will see that all the criteria are followed. The Grand Prize is randomly assigned to three doors, the first choice is made randomly, and Monty opens the door avoiding the contestant's first guess and the door with the Grand Prize. Then the contestant always switches to the other available door. So this spreadsheet is playing the Classical Monty Hall Game where the contestant always switches doors.
If you want to see the actual implementation in the spreadsheet (if you have Excel or a spreadsheet that opens Excel files), you can click here. That way you can diddle with the equations and number of times the game is played (Here the percentage is calculated by averaging the number of 1's in the column that tallies up the wins. This makes it invariant to the number of games provided the averaging includes all the lines that represent games).
And what you'll see is that out of 1000 Monty Hall Problems we had 674 or 67.4 % of the games where the contestant who switched won the Grand Prize. If we run a total of 30,000 tests (and using some other techniques that do go beyond middle school math), we can show us that the actual probability at 95 % confidence is 66.3 % +/- 0.8 %. It takes a bit more work and is not really worth the extra effort, but if we play the game 5,000,000 times, we find the number of games won is 66.69 % +/- 0.035 %, and so the theoretical percent of 66.666666666...%, etc., etc. falls in the uncertainty range.
So we've confirmed the 2/3 probability for changing the doors is indeed correct.
How about that?
¡Un Explanación, Por Favor!
It's all well and good to go through the math, but why do people still have trouble accepting what is a conclusively proven answer, that is, that you should always switch? Well, it's because, as we said, it's just a bit strange. But the strangeness becomes less if you understand what's actually happening.
Where people have problems is that because the Grand Prize is randomly assigned to a door and the contestant randomly makes a selection, they somehow think Monty is also randomly opening his door as well. That is not true, of course. Remember, 2/3 of the time Monty must needs have (as Henry VIII might have said) leave the door shut that has the Grand Prize.
This means that because he knows where the Grand Prize is, most of the time he is actually giving the answer away by keeping the door shut. Monty's knowledge of where the Grand Prize is then tips his hand and he reveals - 2/3 of the time - where the Grand Prize is.
So pick that door he leaves shut!
The Real (Sort of) Monty Hall Problem
What we've seen above is the Classic Monty Hall Problem. And we see it favors the contestant if they switch doors. But what we've shown - the "Classic" Monty Hall Problem is not - let's repeat, that's NOT! NOT! NOT! - the way the game was actually played. At least not when they got to the end of the show where they had the Big Deal.
At the end of the show, Monty would go to the contestants who had won some earlier prize and ask if they wanted to risk their winnings for the Big Deal. There were three prizes behind the three doors. Usually one prize was a Booby Prize, the other a Nice Prize, and the other was the Big Deal (the Grand Prize), which was typically a vacation to a hot spot like the Riviera or a cruise to the Caribbean.
Usually Monty could find at least two contestants willing to take the risk. But he would asked each contestant to pick a different door. But he did not give them the option to change their minds.
Naturally, this type of game makes a boring numerical brain teaser since the odds for each contestant is 1/3 that they picked any one of the prizes. So the usual Big Deal as actually played doesn't even make a brain teaser at all.
But what if Monty did give them the option to switch? Well, it doesn't make any difference. You can "prove" this by simply saying that since the initial odds are 1/3 for any prize, and no one with knowledge makes any intermediate decisions, the odds remain 1/3 no matter what they do. This answer is true enough, but such simple reasoning also seems similar to what gave us the wrong answer for the Classic Monty Hall Problem. So we'll step through the odds as we did before.
OK, take the first scenario (and remember, Contestant #1 always switches doors). Suppose Contestant #1 picked the door with the Grand Prize (at odds 1/3). So the odds that Contestant #2 picked the Nice Prize given that Contestant #1 has already picked the Grand Prize are now 1/2 since there are only two choices left. The odds that the contestants make this particular selection - are 1/3 X 1/2 = 1/6.
So when Contestant #1 switches, he cannot pick the Nice Prize, but must pick the Booby Prize (conditional probability = 1). So the odds are 1/6 X 1 = 0 to win the Nice prize and 1/6 X 1 = 1/6 to win the Booby Prize. (Of course, since Contestant #1 switches, the odds are also zero to win the Grand Prize).
Similarly if Contestant #1 picked the door with the Grand Prize and Contestant #2 picked the Booby Prize, the odds for the Nice Prize are 1/6 X 1 = 1/6 and 1/6 X 0 = 0 for the Booby Prize.
But what if Contestant #1 picks the Nice Prize, and Contestant #2 picks the Grand Prize? Well, after Contestant #1 switches, the odds are 1/6 X 1 = 1/6 for to pick the Booby Prize, 1/6 X 0 = 0 to pick Grand Prize.
Then if Contestant #1 picks the Nice Prize, and Contestant #2 picks the Booby Prize, the odds become 1/6 X 1 = 1/6 to pick the Grand Prize, and 1/6 X 0 = 0 to pick Booby Prize.
Finally if Contestant #1 picked the Booby Prize and Contestant #2 picked the Grand Prize, when Contestant #1 switches, the odds are 1/6 X 1 = 1/6 to pick the Nice Prize and zero for the Booby Prize. If Contestant #2 picked the Nice Prize, the odds for Contestant #1 are 1/6 X 1 = 1/6 for the Grand Prize and zero for anything else.
We've specified all the cases for Contestant #1 switching doors. Summing them up, we get:
Grand Prize = 0 + 0 + 0 + 0 + 0 + 0 + 1/6 + 0 + 0 + 0 + 1/6 + 0 = 1/3
Nice Prize = 0 + 0 + 1/6 + 0 + 0 + 0 + 0 + 0 + 1/6 + 0 + 0 + 0 = 1/3
Booby Prize = 1/6 + 0 + 0 + 0 + 1/6 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 1/3
As Flakey Foont asked Mr. Natural, "What does it all mean?" Well, if you want play the game as on the original show and want to change doors, to paraphrase Mr. Natural's famous reply, it doesn't matter.
Cultural Values and Monty Hall
The best way to explain the apparent contradictions between the Monty Hall Problem and the Real Monty Hall Problem is to realize they are actually equivalent but differ due to cultural values. A strange explanation but one that we will show to be correct, if you consider the Classic Problem from a standpoint of a culture where the concept of wealth is different than ours.
For instance, suppose the contestant is a Biblical patriarch. For him gold, silver, televisions, new kitchens, new sofas, mink coats, and vacations to Rio would be worthless. What good would all that [stuff] be for a Middle Eastern nomad 800 years before the birth of Christ?
No, for Abraham, Isaac, Jacob, and their friends, wealth was counted in sheep and donkeys. In other words, put them on Let's Make a Deal, they'll prefer what we call the Booby Prize.
So you see where we are. If our patriarch is playing the Real Monty Hall Problem, then in his opinion he is playing the Old Monty Hall Problem of the math publications! That is, he sees there are two Booby Prizes - what we call the Grand Prize and the Nice Prize - and one Grand Prize which is the donkey. The math is the same and if he switches he'll get the donkey with 2/3 probability and 1/3 for the Grand Prize. If Monty sticks with the rules for the Real Monty Hall Problem, our Patriarch never wins the Nice Prize.
But what if Monty does opt to reveal the Grand Prize as well as the Nice Prize? Again it doesn't matter - for the Patriarchs it's still two Booby Prizes and one Donkey Grand Prize. The only differences he gets the Grand Prize 1/6 of the time, the Nice Prize 1/6 of the time, and the donkey 2/3 of the time.

The culture is different. / The math is the same.
References
"A Problem in Probability", Steve Sellvin, American Statistician, Vol. 29, No. 1, p. 67, 1990. The problem as posed in this original article was set up with Monty showing the contestant three boxes. One had the keys to a new car and the other two were empty. This would be much more like what you would really have seen during Let's Make a Deal, but for some reason the problem got the problem confused with the Big Deal at the end of the program.
"The Game Show Problem", Marilyn Vos Savant, Parade, September 9, 1990. The question was posed as saying there were the three doors, one with the car and the other two with the goats. But as the problem began circulating, donkeys became popular.
Weird Water & Fuzzy Logic: More Notes of a Fringe Watcher, Martin Gardner. A collection of Martin's columns which includes a discussion of the Monty Hall Problem and how Marilyn's column provoked such outrage. Despite how simple the actual proof of the correct answer is, the controversy did not die down for quite a while and one commentator pointed out that Marilyn's answer must be wrong because it would be ridiculous for 1000 Ph. D. mathematicians to be disagree with her if she was right.
Martin's column on the "Three Prisoners" - essentially a mathematically equivalent problem - was published in his "Mathematical Games" column in the September 1959 issue of Scientific American.
"Monty Hall Revisited", Keith Devlin, http://www.maa.org/devlin/devlin_12_05.html. A variant that was actually closer to how the game was played. And in that case - ergo, when you have two contestants each picking a door. It doesn't matter if they change or not. Besides, usually they weren't given the option.