Prince Louis De Broglie

(Click to Zoom In and Out)

In a day when graduates of high school have trouble calculating what 10% of $10¹ is, it's no surprise that most of what people really know about quantum mechanics is that it has something to do with a cat. Ask 'em to look at the math behind the mechanics and they throw up their hands in horror.

But what is a surprise to the less mathematically adept is the basics of quantum mechanics can be dealt with most easily. Even the famous Schrödinger equation - from the guy with the cat - is not terribly difficult to derive. And behind that derivation is still another equation that figuring it out doesn't go beyond the simplest of middle school algebra.

The equation deals with what is called wave-matter duality. Despite the rather mystical sounding label, the concept is so simple that people scratch their heads and wonder. For this, they ask, Prince Louis Victor Pierre Raymond de Broglie, le septiéme duc de Broglie, won the 1929 Nobel Prize? Well, yes, it is, and it may be the veritable simplicity that merited the award.

Louis's equation is probably the most fundamental equation of quantum mechanics, second only to that of Max Planck about the quantization of light. In fact, Louis borrowed Max's equation and also one by some chap named Albert.

That's Albert Einstein, of course. And Albert wrote probably the most famous equation in history. That is:

m

=

L/V2

Of course, that's not the way most people write the equation today. Instead it's:

E

=

mc2

... which is probably what you've seen.

Of course, we all know that the letter m represents the amount of mass that is equal to the energy, E, and the letter c is the speed of light, which is exactly 299792458 meters per second² (or in miles per hour, that's 670,616,629 miles 2,029 feet 7 inches ²⁷⁵⁵⁹/₁₀₀₀₀₀ inches approximately).

Less familiar - unless you've taken high school physics or chemistry - is Max's equation.

E

=

hν

Here again the letter E is the energy, but in this case it's the energy in a quantum³ of light or photon whose frequency is represented by the Greek letter nu, ν⁴.

So here's where Louis got to work. In the original publication about m = ^L/_V² - or rather E = mc² - Albert was not referring to some hypothetical equivalence. He was saying that if a body gives off radiation with energy E, then the real measurable mass of the body decreases by E/c².

And Louis figured out was that you can take Max's equation about energy of light and put it together with Albert's equation of lost mass. That is, the obvious equation:

E (loss of mass)

=

E (of emitted radiation)

... which is the same as writing:

mc2

=

hν

Now from the equations of waves we know that the frequency, ν, of light - the numbers of cycles per second - is equal to the speed of the wave - in this case, c - divided by the wavelength, λ:

ν

=

c/λ

... and rewrite the equation as::

mc2

=

hν

... as:

mc2	=	h(c/λ)
	=	hc/λ

Now divide both sizes by c:

mc2/c	=	(hc/λ)/c
mc2/c	=	(hc/λ)/c

mc

=

h/λ

Since that was so much fun, we'll do it again:

m

=

h/λc

Although we're done we can also write the equation another way by algebraically switching the m and the λ.

λ

=

h/mc

Now at this point it may seem all we've done is simply some mathematical manipulation of numbers. But here Louis made what historians of science call a paradigm shift.

The equation, Louis said, is not just an algebraic manipulation. Any object with mass - an electron, a proton, a triple decker London bus - has an actual wavelength. That means you can replace the speed of light, c, with the velocity of the body, v.

λ

=

h/mv

(Note: Don't confuse the English letter, v, with the Greek letter, ν.

... and our wavelength, λ, is called the de Broglie wavelength for an object with mass m.

For really big objects, like the London bus, the energy is so large that the wavelength is so short that the object doesn't act like a wave. But if you got tiny particles - like electrons - that's something else again.

Louis's equation - which was first published in 1924 - means if you send electrons through slits or diffraction gratings you should get the electron beam to diffract like light waves. And sure enough, some physicists gave it a try and dang if it didn't work.

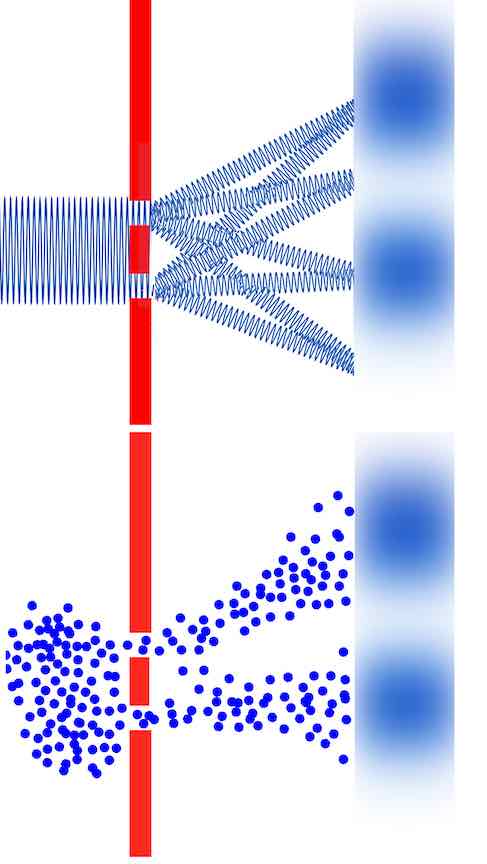
It worked.

Soon Louis's equation was put to a real practical use. Since electrons are more massive than a photon (which has no rest mass) that means electrons have a lot more energy. This means that an electron's wavelength is much shorter than that of visible light.

And electrons can light up a phosphorescent screen. So according to Louis's equation you could "shine" electrons on a small object - much smaller than can be seen with a light microscope - and get a picture. And sure enough, in the mid-1920's people started fiddling with these "electron microscopes". And son-of-a-gun, they worked, too.

OK. So Louis made a discovery that can aid mankind by letting us see bacteria and viruses. But what else can Louis's equation do?

Without doubt the most important use of Louis's discovery was by Erwin Schrödinger. Erwin was a young faculty member in Germany and one story is that one of the senior professors chided him that he wasn't doing anything important. Well, since Erwin wasn't busy, how about giving a lecture on the new hot topic. You know, the one where that French fellow Louis De Broglie predicted that electrons and other subatomic particles actually have a wavelength.

Erwin gave the lecture, but no one was impressed. Huh! How could there be a wave nature of electrons if there was no wave equation for them?

Well, if you needed a wave equation to talk about the wave nature of electrons, then dang it, Erwin decided he'd make a wave equation for electrons. So he began to reason something like this.

Take the classic equation for a wave. This is a nice simple sine wave.

ψ = Asin(^2πx/_λ)

As we know A is the amplitude - how high the wave is - and λ (the Greek letter lambda) - is the wavelength - the distance between peaks or troughs. Of course π is our old friend 3.1415926, etc., etc. The variable x is a position along the wave.

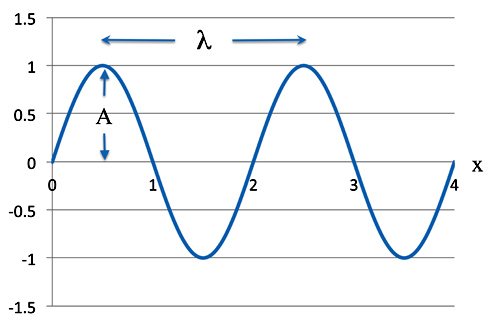
(Click to Open in New Window)

Well, Erwin said, let's first take the derivative of the wave with respect to position just like you did in middle school calculus (well, all right, high school calculus).

^dψ/_dx = Acos(^2πx/_λ) × ^2π/_λ

Since that was so much fun, Erwin did it again.

^d2ψ/_dx² = -Asin(^2πx/_λ) × ^2π/_λ × ^2π/_λ

Now group the various parts together.

^d2ψ/_dx² = ^-4π2/_λ²Asin(^2πx/_λ)

At this point you'll notice that there's part of the equation that is just the original equation for the wave.

^d2ψ/_dx² = ^-4π2/_λ²Asin(^2πx/_λ)

But since our sine equation was written as:

ψ = Asin(^2πx/_λ)

We can now write everything more succinctly.

^d2ψ/_dx² = ^-4π2/_λ² × ψ

This is indeed a wave equation, a second order differential equation in fact. The solution doesn't necessarily need to be the same sine wave. Any function that works, well, works.

At this point, there is nothing really new. Wave equations have been around as long as there has been calculus and waves. And they have many different solutions.

But here Erwin took Louis's equation:

λ = ^h/_mv

... and the wave equation:

^d2ψ/_dx² = ^-4π2/_λ² × ψ

... and simply substituted Louis's equivalent for wavelength - that is h/mv - for the wavelength in the equation, λ.

... and you get:

^d2ψ/_dx² = ^-4π2/_(h/mv)² × ψ

Now with some middle school algebraic gymnastics:

^{d2ψ/_dx2 = -4π2m2v2/_h2 × ψ}

^d2ψ/_dx² = ^-4π2m(mv2)/_h² × ψ

^d2ψ/_dx² = ^{-8π2m(½mv2)}/_h² × ψ

Now note that at one point we have the expression ½mv² in the equation.

^d2ψ/_dx² = ^{-8π2m(½mv2)}/_h² × ψ

Again from middle school you'll remember this is the equation for kinetic energy which physicists like to represent using T.

T = ½mv²

(T is probably an abbreviation of the French travail mécanique or quantité de travail but no one's really sure.)

So put the T into the equation and perform some more algebra:

^d2ψ/_dx² = ^-8π2mT/_h² × ψ

-(^h2/_8π²m)^d2ψ/_dx² = Tψ

At this point we have to remember (again) that the total energy of a system is the sum of the kinetic and potential energy.

E = Kinetic Energy + Potential Energy

which we represent as:

E = T + V(x)

The x in the V(x) is to show that potential energy is a function of the position of the electron.

We now rewrite our last equation as:

T = E - V(x)

We can now substitute the expression E - V(x) for T in our wave equation and get:

-(^h2/_8π²m)^d2ψ/_dx² = [E - V(x)]ψ

Which with more algebra gives us:

-(^h2/_8π²m)^d2ψ/_dx² + V(x)ψ = Eψ

And believe it or not we have the Schrödinger equation in one dimension.

At this point, you can calculate energies and positions of electrons as long as they stay on a straight line. But if you want to calculate how electrons behave in space, we need to go to three dimensions.

Which is actually pretty easy. Just add in the y and z coordinates like we have for the x coordinate and substitute the partial differential sign, ∂, for the single variable differential, d.

-(^h2/_8π²m)(∂²ψ/∂x² + ∂²ψ/∂y² + ∂²ψ/∂z²) + V(x, y, z)ψ = Eψ

Hey, presto! You have the time indepdendent Schrödinger equation in three dimensions!

[Note: Erwin was able to take this equation and by using polar coordinates proved you could derive the energy levels of the hydrogen atom which agreed perfectly with the experimental spectrum. For his efforts, Erwin received the Nobel Prize in 1933.]

Now admittedly the Schrödinger equation is a pretty long expression. And when writing textbooks, the authors like to save space. We can do this by coming up with some abbreviations for the more long-winded notation.

So we start off with our last equation which is:

-(^h2/_{8π²m)(∂²ψ/∂x² + ∂²ψ/∂y² + ∂²ψ/∂z²) + V(x, y, z)ψ = Eψ}

Now the conventions of calculus let us rewrite this as:

-(^h2/_8π²m)(∂²/∂x² + ∂²/∂y² + ∂²/∂z²)ψ + V(x, y, z)ψ = Eψ

Which means we have defined an operator as:

∂²/∂x² + ∂²/∂y² + ∂²/∂z²

That is, we understand that if you write this expression in front of a function it means to take the second derivative with respect to the position of the electron coordinates x, y, and z.

Let's simplify things further by defining the symbol ∇² as:

∇² = ∂²/∂x² + ∂²/∂y² + ∂²/∂z²

And we now have:

-(^h2/_8π²m)∇²ψ + V(x, y, z)ψ = Eψ

Or equivalently

-(^h2/_8π²m)(∇² + V[x, y, z])ψ = Eψ

And if we can abbreviate further with:

-(^h2/_8π²m)(∇² + V[x, y, z]) = H

where H is the famous Hamiltonian operator. So after all this we now have the Schrödinger equation as:

Hψ = Eψ

So with Louis's discovery, a simple wave equation, and some middle school math, you get one of the most fundamental equation of the Universe.

How about that?

References

"Louis Victor Pierre Raymond duc de Broglie", J. J. O'Connor and E. F. Robertson, MacTutor, May 2001.

"The Schrödinger Equation", Chemistry, LibreTexts.

Return to CooperToons Caricatures

Return to CooperToons Homepage