Abraham Robinson, Hyperreal Numbers, and Infinitesimals
Making it Easy

Abraham Robinson
He made it easy.
A Modern Tradition
If you've ever taken a modern calculus course, you probably did OK when calculating derivatives and figuring out the integrals. That is, as long as you didn't have to prove how to calculate derivatives or figure out the integrals.
Actually, proving formulas for derivatives and even integrals wasn't the problem. It was trying to prove the limit of a formula using the dreaded epsilon-delta notation that drove you nuts. Sadly, the inventors of calculus who used simpler systems - Isaac Newton, Gottfried Leibniz, and Seki Takakazu - lacked the rigor demanded by later mathematicians. So came the 20th century and incomprehensibility.
But we, on the other hand, would like to see how to do calculus without using limits - provided, of course, it is with sufficient rigor.
I thought you would as Captain Mephisto said to Sidney Brand. It's very simple really.
And, yes, it was Abraham Robinson who showed us the way. He was, as you'll figure out if you read on, one of the more inventive mathematicians of the 20th century - literally. He decided that if the current numbers wouldn't do the job, then he'd just invent numbers that would. By the way, if you didn't reach this page through the usual CooperToons Caricature introduction, you can read a bit about Abraham's interesting - and for a mathematician rather adventurous - life if you click here.
To show that Gottfried, Isaac, and Seki really did know what they were talking about, Abraham had to invent a new kind of number. Of course, it's a moot point if Abraham invented the new numbers or if he discovered them. Platonists believe numbers exist independently of the human mind. Others, though, think numbers are a human and therefore artificial construct. But in any case, the new numbers Abraham wrote about are most unusual.
We'll start out simply. Everyone knows what counting numbers are. They're just 1, 2, 3, ... and on up. These are also called natural numbers and they make up a set designated as N.
And if you take the counting numbers and stick in the number zero (0) and allow the option of the minus sign, you have integers. These make up a set mathematicians represent - not as I, but Z.
And you certainly know you can take the integers and put one on top of another separated by a line, ½, ¼, ⅔ , -⅔ , -¼ and such. These, of course, are fractions. Since fractions are ratios of integers they are called rational numbers.
But notice that some rational numbers are counting numbers and integers: 1/1 , 2/1 , -8/4 , and so on. We say that counting numbers and integers are subsets of the rational numbers.
But then you have numbers like π (3.14159...), the square root of 2 (√2 or 1.41421...), and the famous exponential number e (2.71828.....). These are irrational numbers. And if you lump the irrationals with the rationals, integers, and counting numbers, we have the real numbers. The real numbers are symbolized by R.
We see then that the simpler systems are subsets of the more complex systems.
N ⊂ Z ⊂ Q ⊂ R
So you might suspect you could represent the complex systems in terms of the simpler ones.
And you would be right. First of all, all of these numbers can be represented as combinations of the 10 digits (0, 1, 2, 3, 4, 5, 6, 7, 8,9) plus a few more signs (. , + , -). For instance, counting or natural numbers are the numbers greater than zero that you can write using the digits followed by a decimal point and nothing but zeros.
| 1 | = | 1.00000..... |
| 2 | = | 2.00000..... |
| 3 | = | 3.00000..... |
| 4 | = | 4.00000..... |
| 5 | = | 5.00000..... |
And integers just have positive or negative signs added and include zero.
| -3 | = | -3.00000..... |
| -2 | = | -2.00000..... |
| -1 | = | -1.00000..... |
| 0 | = | 0.00000..... |
| +1 | = | +1.00000..... |
| +2 | = | +2.00000..... |
| +3 | = | +3.00000..... |
Rational numbers are represented like integers except that to the right of the decimal point, you have lists of digits that either come to an end - they terminate - or repeat endlessly.
| 1/2 | = | 0.50000..... |
| 1/3 | = | 0.33333..... |
| 1/4 | = | 0.25000..... |
| 2/3 | = | 0.66666..... |
| 5/3 | = | 1.66666..... |
And irrational numbers don't come to an end or repeat:
| π | = | 3.14159..... |
| √2 | = | 1.41421..... |
| e | = | 2.71828..... |
Now note that there is not necessarily just one way of representing numbers. For instance, the number "1" has two representations.
| 1 | = | 1.00000...... |
| 1 | = | 0.99999...... |
For those who have forgotten their grade school math, you can prove the lower number is the same as the first:
| x | = | 0.99999...... |
| 10x | = | 9.99999...... |
| 10x - x | = | 9.99999...... - 0.99999..... |
| = | 9.00000...... | |
| (10 - 1)x | = | 9.00000...... |
| 9x | = | 9.00000...... |
| x | = | 1.00000...... |
Now we can, if we wish, write our numbers in a different manner. Instead of a decimal point separating sequence of digits, we can adopt a more flexible notation. What was on the left of the decimal point is a single integer of any size, and all other digits are separated by commas:
| 1 | = | 1.00000..... | = | 1 , 0 , 0 , 0 , 0 , 0 , . , . , . , |
| 1¼ | = | 1.25000..... | = | 1 , 2 , 5 , 0 , 0 , 0 , . , . , . , |
| π | = | 3.14159..... | = | 3 , 1 , 4 , 1 , 5 , 9 , . , . , . , |
| 1723⅔ | = | 1723.66666..... | = | 1723 , 6 , 6 , 6 , 6 , 6 , . , . , . , |
And of course we can write negative numbers as well:
| -1 | = | -1.00000..... | = | -1 , 0 , 0 , 0 , 0 , 0 , . , . , . , |
| -1¼ | = | -1.25000..... | = | -1 , 2 , 5 , 0 , 0 , 0 , . , . , . , |
| -π | = | -3.14159..... | = | -3 , 1 , 4 , 1 , 5 , 9 , . , . , . , |
The message to take away is that counting numbers, integers, rational numbers, and real numbers can all be represented simply as sequences of digits and a few more symbols.
Non-Traditional Tradition
OK. But what would you call these lists:
| -1 , -1 , -1 , . , . , . , |
| ½ , ½ , ½ , . , . , . , |
| π , π , π , . , . , . , |
| √2 , √2 , √2 , . , . , . , |
Hm. They are certainly sequences - not of digits - but of actual integers, rational and even of real numbers.
But are these sequences also numbers?
Actually, yes. In fact, they are simply a new way to represent numbers. So to write a counting number, integer, rational number, or real number, in our new system, you just repeat the number:
| Counting: | 1 | , | 1 | , | 1 | , | . , . , . | |
| Integer: | -5 | , | -5 | , | -5 | , | . , . , . | |
| Rational: | ½ | , | ½ | , | ½ | , | . , . , . | |
| Real (Irrational): | π | , | π | , | π | , | . , . , . |
And so to add, subtract, multiply, and divide, you just add, subtract, multiply, and divide the terms in the sequences.
For example, in our system adding π and √2 is simple enough:
| π + √2 | = | π + √2 , π + √2 , π + √2 , . , . , . , |
We can also compare numbers. For instance, consider this sequence:
| ½ , ½ , ½ , . , . , . , |
... which is simply the number ½
... and the number for ¼ is:
| ¼ , ¼ , ¼ , . , . , . , |
So we know that 1/2 > 1/4 because:
| ½ > ¼ , ½ > ¼ , ½ > ¼ , . , . , . , |
And it was Abraham who invented this new system of notation.
A Bit Hyper
At this point you're wondering, what the hey? What's the point of creating a system where a number is just repeating the number?
From this, Abraham made a living?
But hold on there, Pilgrim. What about this number?
| ½ , ¼ , ⅛ , . , . , . , |
You notice that this number is written in our new notation. But the individual terms are not identical. So it clearly isn't a counting number, integer, rational, or real number.
But it can still be added subtracted, multiplied, and divided according to our rules. So it's a number, yes, but what kind of a number?
It is, to use Abraham's term, a hyperreal number. That is, it is a bonafide number but one that is outside of the real number system. Still you can clearly perform all the usual arithmetic operations. But there are a few changes we have to make, particularly if we want to compare a hyperreal number with another.
OK. Suppose we have a hyperreal number we'll call h. And we have another number we'll call k.
Let's also say that in h the first term in the sequence is larger than the first term in k. But at some point along the sequence the terms of h become less than the corresponding term in k.
| h: | h1 | h2 | h3 | ... | hi | ... |
| hi vs. ki: | Bigger | Bigger | Smaller | ... | Smaller | ... |
| k: | k1 | k2 | k3 | ... | ki | ... |
Is h greater or less than k?
Well, there are only a finite number of terms of h that are larger than the corresponding term in k. But h has an infinite number of terms that are smaller than the one for k. So we must conclude that h is smaller than k.
h < k
More generally, for any hyperreal numbers x and y, we say that x < y if for some number i, every term in the sequence xi in x is less than the corresponding term yi in y.
Now here's where things get interesting. Let's go back to the number:
| ½ , ¼ , ⅛ , . , . , . , |
... and we'll let it be h.
Now let's compare h to two real numbers, 0 and ½.
First, zero:
| h: | ½ | ¼ | ⅛ | ... | 1/2i | ... |
| 0: | 0 | 0 | 0 | ... | 0 | ... |
So we see that every term of h is greater than every term in 0. Therefore we know:
h > 0
Now let's compare h to ½
| h: | ½ | ¼ | ⅛ | ... | 1/2i | ... |
| ½: | ½ | ½ | ½ | ... | ½ | ... |
We see h is smaller than ½. That's because there is a value of i (namely i = 1) above which every term of h is less than the corresponding term in ½.
That is, if i > 1, then for every value of i:
1/2i < 1/2
And so by our definition:
h < 1/2
... and we summarize:
0 < h < ½
That raises another question. Just how close is our number, h, to ½? And how close is h to 0?
Well, let's answer both questions together. That is, we'll ask how close any hyperreal number can get to any real number. We'll call the real number ρ.
First, let's just add ρ and h and call it m.
| m | = | ρ + h | = | ρ + ½ , ρ + ¼ , ρ + ⅛ , . , . , . , |
OK. What kind of number is m?
Well, we see that terms of m are not the same. Therefore it is a hyperreal number, not a real number.
On the other hand, let's add another real - but non-zero - number σ to ρ. We'll call the sum n.
| n | = | ρ + σ | = | ρ + σ , ρ + σ + ρ , ρ + σ , . , . , . , |
Since σ is a real number, all it's terms are identical. The terms of the sum are also identical:
Therefore n is also a real number.
Now let's compare n and m. We do that by looking at the individual terms of ρ + h and ρ + σ.
| Number: | n | m |
| Term i | ρ + σ | ρ + 1/2i |
So regardless of the value of σ, there is always a term of m which will be smaller than the subsequent terms of n. So we know:
m < n
... and that both m and n are greater than ρ:
| m | > | ρ |
| n | > | ρ |
And since m, n, ρ, are all greater than zero, we can order our numbers as:
0 < ρ < m < n
And necause:
0 < m = ρ + h < n = ρ + σ
... a little middle school algebra shows us ...
0 < ρ + h < ρ + σ
... and hence...
0 < h < σ
Since σ is any real number we have shown that (and pardon us if we shout):
| ALTHOUGH NON-ZERO AND POSITIVE, THE HYPERREAL NUMBER, h, IS SMALLER THAN ANY REAL NUMBER! |
... or briefly:
0 < h < Any Real Number
Doesn't that sound familiar?
Success!
Yep. The type of number we are talking about is what the old style calculus teachers called an infinitesimal!
h = dx
What is important is our infinitesimal dx is actually a number - and a non-zero number. So we can add it, subtract it, and multiply it. But best of all we can divide it into any other numbers without violating the usual prohbition that you can't divide by zero.
In short, we have just given a rigorous definition of - and justification for using - infinitesimals in calculus!
Infintesimals have interesting properties. For one thing, not all infinitesimals are equal. Some infinitesimals are larger than other infinitesimals. But all are smaller than any real number.
Also clearly there are an infinite number of infinitesimals. And you can add them or subtract them from a real number to get another hyperreal number.
But these new hyperreal numbers themselves are not infinitessimals. They are, though, closer to the original real number than any other real number. That means that every real number is surrounded by what you can call a "cloud" of hyperreals.
So we have seen two types of hyperreal numbers - infinitesimals that are hyper-close to zero and others that are hyper-close to any other real number. But are there other types of hyperreals?
Indeed there are. Remember the infinitesimals are smaller than any real number but they aren't zero. So we can divide our infinitesimal number h into a real number, ρ, and get another number k.
| k | = |
|
What, you ask, is k?
Let's keep it simple and divide h into 1. That is we'll let k be the reciprocal of h.
How do we take the reciprocal? Simple. Just divide the terms as we did before:
| h: | ½ | ¼ | ⅛ | ... | 1/2i | ... | ||||||||
| k (=1/h): |
|
|
|
... |
|
... |
... which we see k is a hyperreal number defined by:
| k: | 2 | 4 | 8 | ... | 2i | ... |
Now compare k to a real number. Let's compare it to 1.
| 1: | 1 | 1 | 1 | ... | 1 | ... |
| k: | 2 | 4 | 8 | ... | 2i | ... |
So any term of k is always greater than that of the corresponding term of 1. That means k > 1.
You can - and you can now prove this for yourself - show that this procedure works for any real number not just 1. So when you divide an infinitesimal into a real number, it produces a hyperreal k that is greater than any real number.
So you might say there are numbers greater than numbers!
You can, if you wish, start fiddling with other hyperreal numbers and come up with other interesting relationships. But certainly the most interesting hyperreals are infinitesimals, and there are some general rules we apply to them.
For instance, if dx and dy are infinitesimals and ρ is a real number, then:
| dx + dy |
| dx × dy |
| dx ÷ dy |
| dx + ρ |
| dx × ρ |
| dx ÷ ρ |
... are also infinitesimals.
By now you can probably fiddle a bit with the definitions of real and hyperreal numbers and prove these relationships. Or at least convince yourself that these equations are true.
OK. So what can we do with the infinitesimals?
Well, let's use infintesimals to find the slope of the tangent line of a function. That is, calculate the derivative.
How about:
y = 3x2 + 2x
The slope, as all who have taken grade school math know, is the rise over run.

Rise Over Run
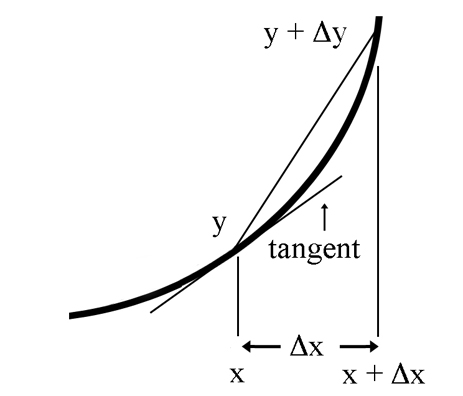
That is, we increase x by an amount Δx
x + Δx
... then the new value of y - which is y + Δy - is given by:
y + Δy = 3(x + Δx)2 + 2(x + Δx)
So the rise over run is:
|
= |
|
And mit ein bischen Algebra:
|
= |
|
||||||
|
|
= |
|
||||||
|
|
= |
|
||||||
|
|
= | 6x + 2 + 3Δx |
But be careful! If Δx is a finite real number we are not calculating the slope of the tangent line to the curve. We are calculating the slope of the line intersecting the two points on the curve, (x , y) and (x + Δx , y + Δy).
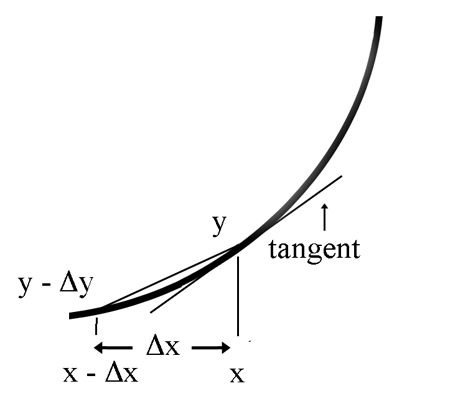
Now suppose we looked at the slope of the line before the value x?
The formula would then be:
|
= |
|
||||||
|
|
= |
|
||||||
|
|
= |
|
||||||
|
|
= | 6x + 2 - 3Δx |
And the slope intersecting the curve at a point x - Δx and x is just:
Slope = 6x + 2 - 3Δx
So what, as Flakey Foont asked Mr. Natural, does it all mean?
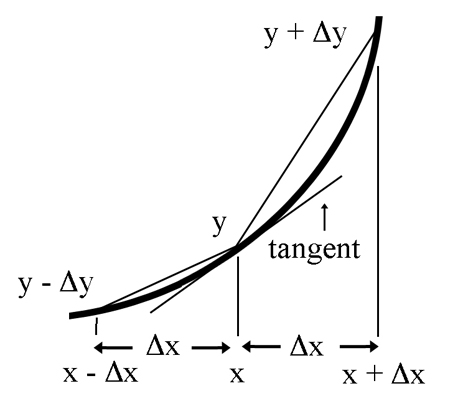
Now we haven't (yet) calculated the slope of the tangent line of the curve. That's because we are using a value of Δx which is a real number. It can be small but it is still a definite real interval.
But we know - and the graph below shows - that the slope of the tangent of the curve 3x2 + 2x at a point x is somewhere between the two values 6x + 2 - 3Δx and 6x + 2 + 3Δx.
But remember what we said. Hyperreal numbers - and so infinitesimals - obey all the rules of arithemtic. So if we had used, not a real number like Δx but an infinitesimal like dx, the formulas would be the same.
And so we would have the both slopes as:
6x + 2 + 3dx
... and ...
6x + 2 - 3dx
... or more succinctly:
Slope(s) = 6x + 2 ± 3dx
But remember, that a constant - like 3 - times an infinitesimal is also an infinitesimal. So using dx rather than Δx, we end up adding and subtracting an infinitesimal from a real number.
But here's the kicker. If a function consists of all real numbers, then the slope of the tangent is a real number. We know that from other math theorems.
And so we know that the slope of our function - that is, the derivative of 3x2 + 2x - is a real number between 6x + 2 plus and minus an infintesimal.
But that means there is no real number closer to the value of our slope than 6x + 2.
And that means that for the function 3x2 + 2x, the derivative is:
Slope = dy/dx = 6x + 2
So - thanks to the work of Abraham Robinson - with the rigorous definition of an infinitesimal, we were able to calculate the derivative of a polynomial.
And calculating the derivative 1) did not use any "neighborhoods" like ε or δ, 2) didn't even use the concept of a limit, and 3) only required middle school algebra.
How about that?
References
"Abraham Robinson", John O'Connor and Edmund Robertson, MacTutor History of Mathematics, St. Andrew University, Web.
Infinitesimal Calculus, James M. Henle and Eugene M. Kleinberg, MIT Press, 1979, Dover, 2002. This book is a good introduction to hyperreal numbers and goes much beyond this brief essay which barely scratches the surface.
Return to Abraham Robinson Caricature