Max Planck
Borrowing from Ludwig
Blackbody Radiation: The Derivation
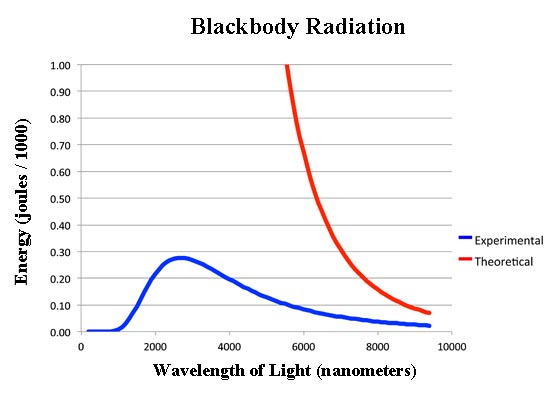
In the 19th century, the theory of blackbody radiation was one of the worst theories ever devised. It was so far off from the experiment you wonder why they even bothered.
Max Planck, though, recognized that the shape of the curve was well known to mathematicians. It was just the x-value divided by an exponential function.
| y | = |
|
... were e is the exponential number, 2.7182818284590452 ... (also called Euler's number) and c is any constant.
The Theory of Blackbody Radiation
You wonder why they bothered.
(Click to open larger image in new window.)
The question was how to get such a simple equation from the then-theory of the day. The trouble was you couldn't. You had to come up with something new.
Actually, Max had some help. One of his friends was Ludwig Boltzmann who like Max was a professor. Ludwig had derived a similar shaped equation by simply figuring out how many ways molecules could shift their energy around. Although the derivation took some tricks and a few steps (which you can see in a new window if you click here), it was nevertheless pretty much limited to what is considered high school mathematics.
Ludwig found that if you had a total of N molecules, the probability that any given molecule, ni, would have a particular energy, εi, is given by:
P(ni) = Ne-kεi/T
... where T is the temperature.
Now if you make a graph of this equation, you'll notice that it doesn't have the right shape. That's because the actual distribution of the energy of the molecules is the equation multiplied by the energy level itself:
D(P) = εiNe-kεi/T
Plot this out and the curve looks OK.
Now the reason Ludwig could get the right equation is that there are only so many molecules in a box. So they can never have an infinite amount of energy. But if you have light or heat waves vibrating in the box there is no limit to how many waves you can have and no limit to their energy. That's why the original theoretical curve of blackbody radiation went up forever as you get to lower and lower wavelengths.
Max realized there was a trick that would work. You just assume the light beams inside the box were acting as "oscillators" that could not assume any energy value. If the energy was restricted to discrete multiples of the wavelength - actually the frequency - then this would produce similar mathematics as having only a finite number of molecules.
So with no other reason except that it would work, Max assumed that the energy of radiation was quantized:
E = nhν
... where n = 1, 2, 3, ... on up.
E is the energy, ν is the frequency of the radiation and h is a constant now commensensically called Planck's constant.
One thing working in Max's favor is that Ludwig's equation applied to anything that had discrete energies. It didn't need to be molecules but "oscillators" would work fine. So Max could start off with Ludwig's basic formula:
ni = Ne-hνi/T
The hope, of course, is that as you got to higher and higher energies, there would be fewer and fewer quanta with those energies. So your equation would start off at zero, rise to a maximum and then drop off.
Now a distinction between Max's equation and Ludwig's is that Max's N is not the total number of quanta. It is the total number of oscillators in the lowest energy state. So Max is not arbitrarily limiting the number of packets as you can for molecules.
Up to this point, we've have engaged in fairly subtle reasoning. Fortunately, from now on out, it's pretty much middle school algebra.
The total energy of all the oscillators, then, is simply made by summing up all the number and their energy levels.
| NTotal | = | N0 + N1 + N2 + N3 ... + Nn + ... |
| = | N0 + N0e-hν + N0e-2hν + N0e-3hν + ... + N0e-nhν + ... | |
| = | N0(1 + e-hν + e-2hν + e-3hν + ... + e-nhν + ...) |
Now to make things simpler you can now write the equation as:
| = | N0(1 + x + x2 + x3 + ... + xn + ...) |
... where x = e-hν
Now, we can do the same thing with total energy of all the quanta as:
| ETotal | = | E1 + E2 + E3 ... + En + ... |
| = | N0hν + N0hνe-hν + 2N0hνe-2hν + 3N0hνe-3hν + ... + nN0hνe-nhν + ... | |
| = | N0hν(e-hν + 2e-2hν + 3e-3hν + ... + ne-nhν + ...) |
... which if you substitute x = e-hν you get:
| ETotal | = | N0hν(x + 2x2 + 3x3 + ... + nxn + ...) |
At this point, we'll remind ourselves that Max's equation does not a priori limit the number of quanta as Ludwig did when talking about molecules. On the other hand if you get to a high enough energy level, the exponential term (x = e-kT/h) gets so small that it cuts off the number of quanta we have (remember that you can only have discrete number of quanta and anything less than 1 means you have no quanta).
So we will ultimately have a finite total number of quanta. And since we are looking for the average energy,
| <E> | = |
|
||||
| = |
|
|||||
| = |
|
We'll skip the details, but as x tends toward infinity, the sums in the numerator, Sn, and in the denominator, Sd, both converge.
| Sn | = |
|
| Sd | = |
|
So you make the substitutions:
| <E> | = |
|
||||
| = |
|
... and canceling out (1 - x), we get:
| <E> | = |
|
... and if you multiply both the numerator and denominator by 1/x we have:
| <E> | = |
|
... which if you remember that x = e-hν/T we now end up with:
| <E> | = |
|
... which if you plot
Max, we remember, thought he was simply coming up with a mathematical trick and that light really wasn't really bundled up in little packets. Today, though, the reality of his quanta - now called photons - is about as undisputable as you can get.
References
"Derivation of Planck's Radiation Law", The Curious Astronomer.
Part 1: https://thecuriousastronomer.wordpress.com/2015/08/06/derivation-of-plancks-radiation-law-part-1/
Part 2: https://thecuriousastronomer.wordpress.com/2015/08/18/derivation-of-plancks-radiation-law-part-2/
Part 3: https://thecuriousastronomer.wordpress.com/2015/09/03/derivation-of-the-planck-radiation-law-part-3/
Part 4: https://thecuriousastronomer.wordpress.com/2016/01/07/derivation-of-plancks-radiation-law-part-4-final-part/
The derivation here is essentially that given above and is probably the best derivation of Max's equation.