Paul Dirac

First of all, anyone learning about M. Paul Dirac figures he must be from the continent. And so they wonder just how you should pronounce his name.

The complete unvarnished and incontrovertible TRUTH is that Paul Adrien Maurice Dirac was

...although Dirac is indeed a French name. And in French it's something like "DEE-rock". But English speakers - which does include the occasional American - will say "deer-ACK".

As we'll see, Paul's family patois might have tended toward the French rendering. But the Anglicized pronunciation didn't seem to bother Paul since that's the way his colleagues at Florida State University pronounced it.

Yes, Florida State University. Paul had spent 37 years as the Lucasian Professor of Mathematics at Cambridge University. This is the most prestigious college professorship for the mathematically inclined and was the same post held by Isaac Newton and Stephen Hawking.

There was, though, a mandatory retirement age and afterwards Paul had visited FSU in north Florida with his wife, Margit (called Manci by her friends). They both really liked the area and so Margit privately asked one of the professors if they might be interested in hiring Paul on the faculty. One author pointed out that was kind of like asking an English department if they'd be interested in hiring Shakespeare, and so Paul came to FSU¹.

Paul Dirac was born in 1902 to a middle class, but hardly typical family. His father, Charles, was born Swiss and of - yes - French ancestry. Charles, who was a French teacher, insisted that Paul speak to him in French.

Paul's mother, on the other hand, was English and spoke to him in English. So to avoid the Din of Babel, Paul and his dad ate dinner in one room and spoke French, and his mom and his brother and sister ate dinner and spoke English in another.

We said that his dad insisted Paul speak to him in French. Actually he insisted Paul speak to him in perfect French. If he made a mistake, Paul's dad would deal with him most severely.

Not surprisingly Paul became quite taciturn. There are stories that someone would ask him a question. Paul would wait for five minutes and then say "Yes", "No", or "I don't know."

Paul didn't start off wanting to be one of the most notable theoretical physicists in history. He first studied electrical engineering at the University of Bristol. But after getting his degree and taking a summer job, he had trouble finding permanent employment probably because if you take five minutes to answer each question during an interview they'll pick someone else. So Paul decided to keep going to school. He then returned to Bristol to study math (or "mathS" as the British say) and he then applied to Cambridge.

We must admit that professors have different standards for hiring than industrial engineers. So Paul passed muster at Cambridge and decided to switch to theoretical physics. At that time - the early 1920's - the big topic was Einstein's Theory of Relativity and it had grabbed Paul's attention.

There is an irony about Paul going to Cambridge. To get admitted to the bachelors programs, you had to know Latin or Greek which Paul had avoided. So although he was accepted for Ph. D. studies at Cambridge, he wouldn't have been admitted as an undergraduate².

But there was another hot topic at the time other than Relativity. That was quantum theory.

Quantum theory started off in 1900 when the German physicist Max Planck was able to explain black body radiation - the intensity of the wavelengths emerging from an externally heated oven - by assuming light energy wasn't continuous but came in discrete packages or quanta of energy. There was no reason for the assumption other than the theory fit experiment.

Then in 1905 Albert Einstein - among other accomplishments that year - applied Max's quantum theory to the photoelectric effect - the observation that certain metals emit electrons when you shine light on them. If light wasn't quantized, Albert couldn't explain the photoelectric effect. If it was, he could. This discovery, not the Theory of Relativity, was to land Albert his Nobel Prize.

Then eight years later the Danish physicist Niels Bohr proposed a theory for the structure of the atom. Niels said that electrons only circled the nucleus in distinct orbits of specific energies. The movement of the electrons from one orbit to the other explained the way atoms emitted and absorbed light. Once more without the quantized energies, you couldn't explain atomic spectra.

All of these theories were proposed more or less to explain heretofore unexplainable phenomenon but there was no underlying theory³. Then in 1925, the German physicist Werner Heisenberg produced a theory of quantized sub-atomic particles. Although to do so he had to propose the famous Heisenberg Uncertainty Principle that states you can't exactly measure the speed (actually momentum) of a particle and its position at the same time.

Werner's paper was difficult even for experts to follow not the least reason being his use of matrices in a form called matrix mechanics. But difficult as Werner's paper was, it did explain subatomic physics better than classical, non-quantized, mechanics and was dubbed quantum mechanics.

Paul was admitted to Cambridge in 1923 and was still a student when Werner published his paper. With his strong mathematical background, Paul recognized mathematical relationships in quantum theory that hadn't occurred to others. He plunged into the topic and ended up with eleven papers published before got his Ph. D. - that's a lot for a graduate student even by today's publish or perish standards. He got his Ph. D. in 1926 with his thesis titled Quantum Mechanics.

Paul then went on to do post-doctoral work at the University of Göttingen with Max Born. Max, in addition to lending half his name to the Born-Oppenheimer approximation that simplifies quantum mechanical calculations for molecules, was the grandfather of pop singer Olivia Newton-John.

Soon Paul began traveling around the world giving lectures. Sometimes he'd appear with Werner which shows how quickly Paul was recognized as a leader in theoretical physics. By 1930, only four years after getting his doctorate, Paul was elected a Fellow of the Royal Society.

Paul remains most famous for his derivation of (what else?) the Dirac Equation. What the Dirac Equation does is combine Paul's two big interests, quantum theory and the Theory of Relativity.

People had tried melding the two theories before. The problem - and pardon if this is splendidly vague - is that time and space are usually thought of something different and even today in most quantum calculations are still treated separately.

In quantum mechanics, the big equation is still the Schödinger equation developed by the famous Erwin Schödinger known today as the inventor of the Cat Thought Experiment. The Schödinger Equation is a differential equation. In fact it's a second order partial differential equation with space - the familiar x, y, and z coordinates - and a first order partial differential equation in time as everyone can see:

-(ħ/m)∇²Ψ + VΨ = i∂Ψ/∂t

Now the ∇² applies only to space - and the superscript 2 means it's a second derivative. But the ∂ (no superscript 2) is a first derivative and as we see is taken with respect to time (t). For those not familiar with the equation, m is the mass of the electron, ħ is the reduced Planck's constant (a fundamental constant of nature), and i is the "imaginary" number which is the square root of -1, √-1. Ψ, of course, is the formula that you're trying to find that fits the equation and so defines the properties of the electron.

Now mixing derivatives is fine if space and time are different. That's the way Isaac Newton saw things and pretty much the way Joe and Josephine Blow on the street see things today.

But the problem is that Einstein's General Theory of Relativity doesn't really distinguish between space and time (you can make time have the same units as space by multiplying by c where c is the speed of light). So if you have a second derivative of space, you should also have a second derivative of time.

In fact, two chaps named Oskar Klein and Walter Gordon tried that out. They took the Schrödinger equation and made a second derivative with time. But the solutions of the Klein-Gordon Equation didn't gibe with experiment.

Paul, as the story goes, was sitting before his fireplace at Cambridge⁴. And it occurred to him if taking the second derivative of time didn't work, why not take only the first derivative of space? You had to make some other changes, but he came up with a pretty simple equation.

-iγ∂Ψ = m∂Ψ

Although the γ is not just a constant but a matrix - that is a grid of numbers, it's a pretty simple matrix. And the main thing to note is that the ∂ means you're taking the first derivative and since we don't specify space or time, the derivative is for both.

And as the American television commercials say, Paul's equation really, really works.

Some have said the Dirac Equation was the most important equation - with the possible exception of Einstein's equations for General Relativity - in 20th century science. It proved that scientific observations that were explained only by after-the-fact/ad hoc explanations were natural occurrences from quantum and relativistic principles.

For instance, one property of electrons is they spin. This property had to be added to Schrödinger wave functions to explain certain atomic properties such as why some lines of atomic spectra come in pairs. But the Dirac equation said electrons should have spin. Paul's equation explained thing so neatly that it landed Paul a Nobel Prize in 1933 along with Erwin.

There were, though, some strange predictions. Paul's equations also said that there were some electrons with negative mass. In principle Paul didn't think negative and positive masses were necessarily more of a problem than negative and positive electric charges. And the reason we never see negative mass electrons, he thought, is they are tucked away in their own energy levels and that the regular electrons with positive mass are what you saw when running experiments.

There were some other strange things that Paul's equation predicted. For instance, consider what happens if you zap an atom with a super-energetic gamma ray. For our reasoning we'll use a very simple model of the atom - just a nucleus surrounded by shells of electrons of specific energies.

Gamma rays penetrate deep into the atom. That means the gamma ray photon (the gamma ray quanta) will knock out an electron from the innermost shell - in Paul's day called the K Shell. Since the atom lost a negatively charged electron it is now an ion with a positive charge.

OK. How do you keep track of the positive charge? A - quote - "modern answer" - unquote - is that you really can't. That's because a net positive charge is simply an imbalance of the protons in the nucleus with the electrons.

Well, then, you might say the newly formed positive charge is in the nucleus. But that doesn't really work. The nucleus always has the same positive charge even when the whole atom was neutral. And if you add electrons - to make a negative ion - there's still the same positive charge on the nucleus.

But Paul's equations found that you could treat the place where you lost the electron as a hole where the electron used to bein' (as Arlo Guthrie might say). That's where the positive charge is.

But you object. That is a totally fictitious positive charge. The charge can't have real existence.

Well, as a former US President who liked to pull his dogs' ears said, let us reason together.

Now what will happen if you do have this fictitious positive charge in the innermost atomic orbital? Well, an electron from the next highest shell - the L Shell - will drop down and fill the hole where the (fictitious) positive charge is.

But that means you now have a (fictitious) positive charge in the next highest electron - the M Shell. That (fictitious) positive charge will then be replaced by an electron dropping from the N Shell. This process keeps going and eventually the fictitious positive charge ends up at the outermost shell of the atom.

What happens then? The atom with the positive charge in the highest electronic shell can pick up an electron from somewhere else. This means the fictitious postive charge has - like a fictitious subatomic Elvis - left the atom. And with more and more electrons available outside the atom, the postive charge - fiction though it is - keeps going further and further from the atom. Oddly enough, this makes perfect sense. The positively charged nucleus should repel any positive charge and keep pushing it further and further way - whether the positive charge is real or not.

And now consider. This charge which doesn't really exist is acting exactly like an electron but an electron with a positive charge. After all, it occupied a shell of an atom and it was jumping through the atom's electron shells. This is exactly what electrons do - except that the "positive electron" is repelled by the nucleus not attracted to it.

But what, just what, if Paul's imaginary postive charges aren't that imaginary? That would mean there are particles that act like electrons but are positively charged.

Naturally Paul published his paper about his equation's predictions - although it wasn't as simple minded as stated here. As you expect people said ha! ha!, ho! ho!, what a funny idea!

It wasn't just the hoi polloi who were smirking behind their hands. First class physicists like Niels Bohr and Wolfgang Pauli (who first deduced that electrons had spin) made considerably merry of Paul's idea. Niels said the theory was a great way to catch an elephant. You'd write up a poster with Dirac's theory and put it by a watering hole in Africa. The elephants would come up and start to read the poster. They would be so amazed at the outlandish ideas that you could slip up behind them and throw a rope around their legs.

Wolfgang, on the other hand, decided that the negative electrons would move so fast that they would fill in the positive holes with such a burst of energy that it would annihilate everything - including theoretical physicists. So the fact theoretical physicists exists proves Paul's theory can't be correct.

Yes, how funny Paul could be.

But the year after Paul reported the idea of his positive electrons, Carl Anderson, an experimental physicist at Cal Tech was looking at electrons that came from outer space. Or rather he was looking at photographs of the tracks of the electrons in a cloud chamber. And he noticed when the electrons from outer space were sent between a magnet only half went off in the direction that a good (negative) electron should. The others went the other direction. So we must conclude that half of the electrons were acting

At the time Carl ran his experiments, he hadn't read Paul's paper. Instead, he thought he might have made a mistake. Still in 1932, he published the finding anyway. Four years later he got a Nobel Prize for the discovery of the positive electron or the positron.

With the discovery of the positron, the discovery of other anti-particles followed. So this led to the concept of anti-matter. And today everyone has heard of anti-matter and think nothing is strange about it. And Paul thought of it first.

And even Paul's idea of negative mass might not be so crazy and now people know not to dismiss a concept out of hand when it pops out of Paul's equation. And sure enough, recently there have been physicists who report creating a fluid which acts like it has negative mass. That is, push on it in one direction, and it accelerates in the opposite direction. And today you'll read a lot about "dark matter" which makes the universe expand at a faster and faster rate. Negative mass might explain what is at present a debated topic.

One of Paul's physicist friends was Eugene Wigner whose contributions to science are considerable but not well known to the general public. Paul's had met Manci because she was Eugene's sister.

If there was someone who was the antithesis of Paul, it was Manci. While Paul almost never talked, Manci talked all the time. Paul had difficulty making friends; for Manci it was a second nature. Paul's biographer said that she was his anti-particle. They got married in 1937.

People who knew Manci would often refer to her as "Wigner's Sister" and that became kind of a nickname. The story is one of Paul's friends came to visit and hadn't heard that Paul had recently gotten married. After he sat down a lady came in to serve them their tea and then sat down with them. Paul's friend greeted the lady and then Paul exclaimed, "Oh, I am sorry. I forgot to introduce you. This is Wigner's Sister - who is now my wife."

Paul died in 1984. You'd think he'd be given a state funeral in England. He could have if he had wanted it. But he was buried in Tallahassee, Florida, as was Manci who lived until 2004.

But there's one final point to note about Paul's discoveries that is often forgotten. And it's about one of the most confusing educational topics to students of, not physics, but chemistry.

A brief refresher of high school chemistry may be in order. If you paid attention in class, you will have learned that the electrons are distributed in atomic orbitals. These are called names like 1s, 2s, 2p, 3s, 3p, 3d, and on up and not just in the old-fashioned shells, K, L, M, etc. Although the 1s orbital is the same as the K shell, the L shell is made up of the 2s and three 2p orbitals. The M shell is made up of the 3s, three 3p, and five 3d orbitals. You can keep going forever.

Orbitals we must say are not orbits. Orbits are specific circular or elliptical paths that a particle takes around a point. The paths of planets around the sun are orbits. But orbitals are not the paths the electrons take in circling around the atomic nucleus. Orbitals don't define a path and don't even have well-defined boundaries.

Instead according to the most common interpretation, orbitals are merely the probability where you'll find electrons of a particular energy at a certain spot.

The orbitals, then, do tell us the energy of the electron but they only tell us the probability of it's position. It's as if the electrons are smeared over the orbitals. And that actually makes sense

For instance, let's take a look at a hydrogen atom with an electron with a kinetic energy of 13.6 electron volts (that's eV for short). This is what it is for the first (or 1s) orbital. 1 eV is equal to 1.602 × 10^-19 joules or 3.83 × 10^-23 calories. That means that an electron in the 1s orbital can heat up 1 gram of water - about 1/5 the weight of an American nickel - not quite 0.00000000000000000000004 degrees centigrade. That's 0.00000000000000000000007 degrees Fahrenheit.

With this in mind, if you use the formula for kinetic energy:

Force = ½mv

... and let the electron circle about a nucleus at a radius of 0.000000002 inches, the electron would be moving in a complete circle in about 0.0000000000000002 seconds. So if we round up to 0.000000000000002 seconds, the electron is at all points on the orbital.

In other words, the electron is smeared out all over its path. And the electron density around the nucleus is dictated by where the electron spends most of its time. And it's the solutions of the Schrödinger Equation that tell us where the electron spends its time by giving us mathematical formula for the individual orbitals.

When students begin to study atoms and atomic structure they find something strange. The solutions to the Schrödinger Equation not only tell us where the electrons can be but where they can't be. The electron forbidden locations are called nodes and there is zero probability that an electron can appear at a node.

Except for the lowest orbital - the 1s orbital - all orbitals have nodes. The easiest nodes to visualize are those in the dumbbell shaped p orbitals - which are planes that extend from minus-infinity to plus-infinity and divide the atom in half (although in the picture only part of the plane is shown).

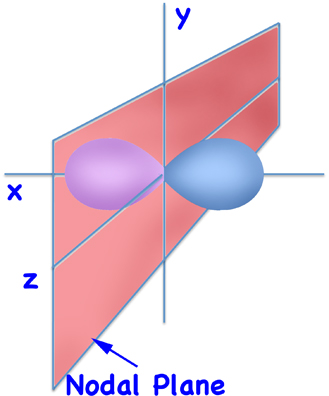
2p_x Orbital
(Schematic)

But we said that orbitals aren't orbits. Instead, if you plot the probability of finding for the 2p orbital you get something like:

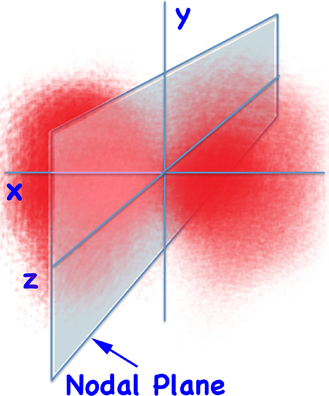
2p_x Electron Density

... and the node separates the two lobes.

But other nodes are spheres that surround the nucleus at certain distances. These are in the s orbitals. Except for the nodes, electrons can be anywhere else. That is, an electron can be on any side of the node at any particular time.

The exception that orbitals have nodes is the one of the lowest energy, the 1s orbital. It has no node. Then if you actually plot the electron density around the nucleus you'll get a picture like:

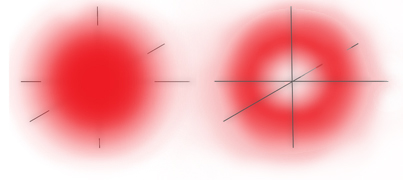
1s Orbital Probability Electron Density
Outside View (Left) - Cross Section (Right)

So the 1s electron can be any distance from the nucleus but it's most likely distance is 0.000000002 inches from the nucleus which happens to be the Bohr radius, that is, the radius of the orbit that Niels deduced in his simplified atomic model⁵.

But now look at the location of electron in the next highest energy orbital, the 2s orbital. If you plot that probability you get this graph:

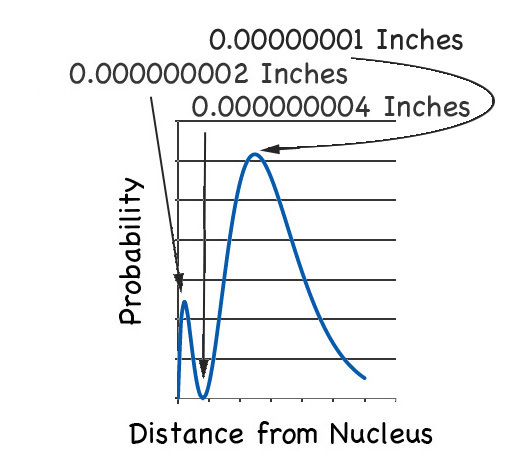
You see that there are two maxima (although one maximum is more maximal than the other). The first maximum is the same place as the 1s orbital, and the other is about five times further on from the nucleus.

But then there is the node between the maxima. If you zoom in on that part you'll find the probability of finding the electron is a big fat:

ZERO

As we see in the zoom:

... and this makes the electron distribution cross section of the orbital looks like:

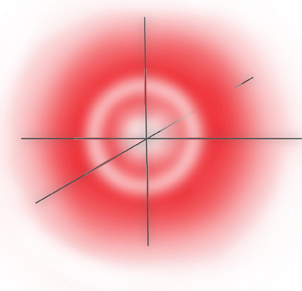
2s Orbital Probability Cross Section

... where the outer band of low probability actually contains the node - a circle of zero probability.

But if there is a finite probability of finding the electron inside the node and a probability that it is outside the node, then the natural question still is:

And now, as the $1000 an hour psychiatrist says, we can begin, yes?

It turns out there are a number of answers to explain the phenomenon of getting past the nodes. And you'll hear them all if you keep asking.

The first answer is that the question is meaningless because you're asking what is the probability that an electron will have zero probability in a plane of zero width. The node has mathematical meaning but no physical meaning.

Therefore no matter how small a volume you pick, even if it includes the node, there's a finite probability that the electron will be in that volume.

But despite the voluble assurances from the teachers, for many students that answer really doesn't answer the question. We know there is a probability the electrons will be on one side of the node or another. But the question was was how does the electron get past that plane of zero probability.

A student who has been reading about quantum phenomenon might wonder if the electron navigating its way past the node is an example of quantum mechanical tunnelling. That means that there is a probability that a subatomic particle will "tunnel" through an area where it normally shouldn't pass through.

But that answer doesn't quite work. Quantum mechanical tunneling occurs only if the barrier - an energy barrier - is finite. The node is not an energy barrier, much less a finite energy barrier.

But if you want a quantum explanation, the teacher might smile and say that the question is a violation of the Heisenberg Uncertainty Principle. We mentioned that the Uncertainty Principle is a fundamental property of nature discovered by Werner Heisenberg (Paul's friend) which states you cannot specify position and energy (actually, the momentum) of a particle with arbitrary exactness. So if you want to know how a particle of known energy gets past an arbitrarily small plane, you must at some point specify the particle's position exactly. And since we're talking about a node of a specific energy, you need to know it's energy (and hence it's momentum) exactly.

But Heisenberg says you can't do that. Specifying the time when the electron crosses the node means you can't pinpoint it's energy. And so you couldn't even tell what orbital the electron is in. Since different orbitals have nodes in different places you can't tell if it's crossing the node you were talking about.

We really can't say that these varied explanations of themselves are necessarily incorrect. But they - as do many quantum "interpretations" - seem to skim past any real explanation. So at this point we can turn to Paul - and get the real story.

Remember, to get the orbitals from Schödinger Equation you simply find functions that fit the equation. And when you find solutions that give you the orbitals of the hydrogen atom, the solutions give you the nodes and there's nothing you can do about it⁶.

But instead of using Erwin's equation - the non-relativistic one - now use Paul's - which includes relativity. There you still get orbitals, and in some cases they look a lot like the Schrödinger wave functions.

Except - and pardon us if we shout:

That is, if you zoom in on the graph of the 2s orbital from Paul's equation, you see this right away.

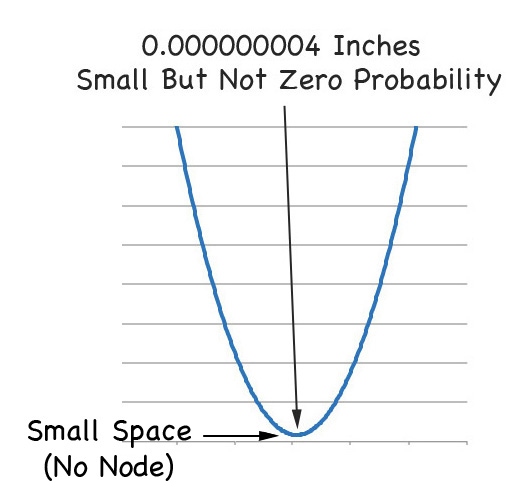
So the best way to think of the Schrödinger Equation is that it's like Newton's Equations. Both ignore relativity but in most cases they do the job. But for the small fine tuning of niggling details you need to include relativity. And when you do that.

We can now resume breathing.

References

The Strangest Man: The Hidden Life of Paul Dirac, Quantum Genius, Graham Farmelo, Faber and Faber, 2009.

"Paul Adrien Maurice Dirac", MacTutor, University of St. Andrews.

Thirty Years that Shook Physics: The Story of Quantum Theory, George Gamow, Doubleday, 1966, Dover, 1985.

"Paul Dirac and the Religion of Mathematical Beauty", Graham Farmelo, Lecture, Perimeter Institute for Theoretical Physics, December 14, 2011.

Legendary Physicist and Florida State Professor Paul Dirac, Florida State University, Film.

"What Exactly is the 'Spin' of Subatomic Particles Such as Electrons and Protons?", Morton Tavel, Scientific American, October 21, 1999.

"Don't Dismiss Negative Mass", M. B. Paranjape, Physics Today, May 24, 2017.

"Most of the Universe is Missing - A 'Dark Fluid' With Negative Mass Could Explain Why", Hannah Osborne, Newsweek, December 5, 2018.

"Wigner's Sisters", Y. S. Kim, ysfine.com.